Формула полной вероятности. Примеры решений задач
Пример №1. Предприятие, производящее компьютеры, получает одинаковые комплектующие детали от трех поставщиков. Первый поставляет 50 % всех комплектующих деталей, второй — 20 %, третий — 30 % деталей.Известно, что качество поставляемых деталей разное, и в продукции первого поставщика процент брака составляет 4 %, второго — 5 %, третьего — 2 %. Определить вероятность того, что деталь, выбранная наудачу из всех полученных, будет бракованной.
Решение. Обозначим события: A — «выбранная деталь бракована», Hi — «выбранная деталь получена от i-го поставщика», i =1, 2, 3 Гипотезы H1,H2, H3 образуют полную группу несовместных событий. По условию
P(H1) = 0.5; P(H2) = 0.2; P(H3) = 0.3
P(A|H1) = 0.04; P(A|H2) = 0.05; P(A|H3) = 0.02
По формуле полной вероятности (1.11) вероятность события A равна
P(A) = P(H1) · P(A|H1) + P(H2) · P(A|H2) + P(H3) · P(A|H3) = 0.5 · 0.04 + 0.2 · 0.05 + 0.3 · 0.02=0.036
Вероятность того, что выбранная наудачу деталь окажется бракованной, равна 0.036.
Пусть в условиях предыдущего примера событие A уже произошло: выбранная деталь оказалась бракованной. Какова вероятность того, что она была получена от первого поставщика? Ответ на этот вопрос дает формула Байеса.
Мы начинали анализ вероятностей, имея лишь предварительные, априорные значения вероятностей событий. Затем был произведен опыт (выбрана деталь), и мы получили дополнительную информацию об интересующем нас событии. Имея эту новую информацию, мы можем уточнить значения априорных вероятностей. Новые значения вероятностей тех же событий будут уже апостериорными (послеопытными) вероятностями гипотез (рис. 1.5).
Схема переоценки гипотез
Пусть событие A может осуществиться лишь вместе с одной из гипотез H1, H2, …, Hn (полная группа несовместных событий). Априорные вероятности гипотез мы обозначали P(Hi) условные вероятности события A — P(A|Hi), i = 1, 2,…, n. Если опыт уже произведен и в результате него наступило событие A, то апостериорными вероятностями гипотез будут условные вероятности P(Hi|A), i = 1, 2,…, n. В обозначениях предыдущего примера P(H1|A) — вероятность того, что выбранная деталь, оказавшаяся бракованной, была получена от первого поставщика.
Нас интересует вероятность события Hk|A Рассмотрим совместное наступление событий Hk и A то есть событие AHk. Его вероятность можно найти двумя способами, используя формулы умножения (1.5) и (1.6):
P(AHk) = P(Hk)P(A|Hk);
P(AHk) = P(A)P(Hk|A).
Приравняем правые части этих формул
P(Hk) · P(A|Hk) = P(A) · P(Hk|A),
отсюда апостериорная вероятность гипотезы Hk равна
В знаменателе стоит полная вероятность события A. Подставив вместо P(A) ее значение по формуле полной вероятности (1.11), получим:
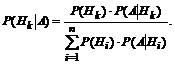(1.12)
Формула (1.12) называется формулой Байеса и применяется для переоценки вероятностей гипотез.
В условиях предыдущего примера найдем вероятность того, что бракованная деталь была получена от первого поставщика. Сведем в одну таблицу известные нам по условию априорные вероятности гипотез P(Hi) условные вероятности P(A|Hi) рассчитанные в процессе решения совместные вероятности P(AHi) = P(Hi) · P(A|Hi) и рассчитанные по формуле (1.12) апостериорные вероятности P(Hk|A), i,k = 1, 2,…, n (табл. 1.3).
Таблица 1.3 - Переоценка гипотез
| Гипотезы Hi | Вероятности | |||
| Априорные P(Hi) | Условные P(A|Hi) | Совместные P(AHi) | Апостериорные P(Hi|A) | |
| 1 | 2 | 3 | 4 | 5 |
H1 — деталь получена от первого поставщика | 0.5 | 0.04 | 0.02 | 
|
H2 — деталь получена от второго поставщика | 0.2 | 0.05 | 0.01 | 
|
H3 — деталь получена от третьего поставщика | 0.3 | 0.02 | 0.006 | 
|
| Сумма | 1.0 | — | 0.036 | 1 |
P(Ω) = P(H1 + H2 + H3) = P(H1) + P(H2) + P(H3) = 0.5 + 0.2 + 0.3 = 1
В четвертой колонке значение в каждой строке (совместные вероятности) получено по правилу умножения вероятностей перемножением соответствующих значений во второй и третьей колонках, а в последней строке 0.036 — есть полная вероятность события A (по формуле полной вероятности).
В колонке 5 вычислены апостериорные вероятности гипотез по формуле Байеса (1.12):
Аналогично рассчитываются апостериорные вероятности P(H2|A) и P(H3|A), причем числитель дроби — совместные вероятности, записанные в соответствующих строках колонки 4, а знаменатель — полная вероятность события A, записанная в последней строке колонки 4.
Сумма вероятностей гипотез после опыта равна 1 и записана в последней строке пятой колонки.
Итак, вероятность того, что бракованная деталь была получена от первого поставщика, равна 0.555. Послеопытная вероятность больше априорной (за счет большого объема поставки). Послеопытная вероятность того, что бракованная деталь была получена от второго поставщика, равна 0.278 и также больше доопытной (за счет большого количества брака). Послеопытная вероятность того, что бракованная деталь была получена от третьего поставщика, равна 0.167.
Пример №3. Имеются три одинаковые урны; в первой урне два белых и один черный шар; во второй — три белых и один черный; в третьей — два белых и два черных шара. Для опыта наугад выбрана одна урна и из нее вынут шар. Найдите вероятность того, что этот шар белый.
Решение. Рассмотрим три гипотезы: H1 — выбрана первая урна, H2 — выбрана вторая урна, H3 — выбрана третья урна и событие A — вынут белый шар.
Так как гипотезы по условию задачи равновозможны, то
Условные вероятности события A при этих гипотезах соответственно равны: 
По формуле полной вероятности
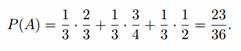
Пример №4. В пирамиде стоят 19 винтовок, из них 3 с оптическим прицелом. Стрелок, стреляя из винтовки с оптическим прицелом, может поразить мишень с вероятностью 0,81, а стреляя из винтовки без оптического прицела, — с вероятностью 0,46. Найдите вероятность того, что стрелок поразит мишень, стреляя из случайно взятой винтовки.
Решение. Здесь первым испытанием является случайный выбор винтовки, вторым — стрельба по мишени. Рассмотрим следующие события: A — стрелок поразит мишень; H1 — стрелок возьмет винтовку с оптическим прицелом; H2 — стрелок возьмет винтовку без оптического прицела. Используем формулу полной вероятности. Имеем
Учитывая, что винтовки выбираются по одной, и используя формулу классической вероятности, получаем: P(H1) = 3/19, P(H2) = 16/19.
Условные вероятности заданы в условии задачи: P(A|H1) = 0;81 и P(A|H2) = 0;46. Следовательно,
Пример №5. Из урны, содержащей 2 белых и 3 черных шара, наудачу извлекаются два шара и добавляется в урну 1 белый шар. Найдите вероятность того, что наудачу взятый шар окажется белым.
Решение. Событие “извлечен белый шар” обозначим через A. Событие H1 — наудачу извлекли два белых шара; H2 — наудачу извлекли два черных шара; H3 — извлекли один белый шар и один черный. Тогда вероятности выдвинутых гипотез
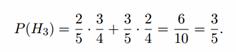
Условные вероятности при данных гипотезах соответственно равны: P(A|H1) = 1/4 — вероятность извлечь белый шар, если в урне в данный момент один белый и три черных ша-ра, P(A|H2) = 3/4 — вероятность извлечь белый шар, если в урне в данный момент три белых и один черный шар, P(A|H3) = 2/4 = 1/2 — вероятность извлечь белый шар, если в урне в данный момент два белых и два черных шара. В соответствии с формулой полной вероятности
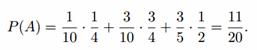
Пример №6. Производится два выстрела по цели. Вероятность попадания при первом выстреле 0,2, при втором — 0,6. Вероятность разрушения цели при одном попадании 0,3, при двух — 0,9. Найдите вероятность того, что цель будет разрушена.
Решение. Пусть событие A — цель разрушена. Для этого достаточно попадания с одного выстрела из двух или поражение цели подряд двумя выстрелами без промахов. Выдвинем гипотезы: H1 — оба выстрела попали в цель. Тогда P(H1) = 0,2 · 0,6 = 0;12. H2 — либо первый раз, либо второй раз был совершен промах. Тогда P(H2) = 0,2 · 0,4 + 0,8 · 0,6 = 0,56. Гипотеза H3 — оба выстрела были промахи — не учитывается, так как вероятность разрушения цели при этом нулевая. Тогда условные вероятности соответственно равны: вероятность разрушения цели при условии обоих удачных выстрелов равна P(A|H1) = 0,9, а вероятность разрушения цели при условии только одного удачного выстрела P(A|H2) = 0,3. Тогда вероятность разрушения цели по формуле полной вероятности равна:
P(A) = 0,12*0,9+0,56*0,3 = 0,276