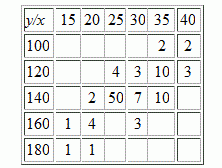Формула Пуассона
Закон Пуассона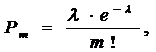
, где λ равна среднему числу появления событий в одинаковых независимых испытаниях, т.е. λ = n × p, где p – вероятность события при одном испытании, e = 2,71828.
Ряд распределения закона Пуассона имеет вид:
| X | 0 | 1 | 2 | … | m | … |
| P | e-λ | λe-λ | 
| … | 
| … |
Назначение сервиса. Онлайн-калькулятор используется для построения Пуассоновского распределения и вычисления всех характеристик ряда: математического ожидания, дисперсии и среднеквадратического отклонения. Отчет с решением оформляется в формате Word.
Числовые характеристики случайной величины Х
Математическое ожидание распределения ПуассонаM[X] = λ
Дисперсия распределения Пуассона
D[X] = λ
Пример №1. Семена содержат 0.1% сорняков. Какова вероятность при случайном отборе 2000 семян обнаружить 5 семян сорняков?
Решение.
Вероятность р мала, а число n велико. np = 2 < 10. Значит случайная величина Х – распределена по Пуассоновскому распределению. Составим закон. λ = 2.
P(5) = λ5e-5/5! = 0.03609
Математическое ожидание: M[X] = λ = 2
Дисперсия: D[X] = λ = 2
Пример №2. Среди семян ржи имеется 0.4% семян сорняков. Составить закон распределения числа сорняков при случайном отборе 5000 семян. Найти математическое ожидание и дисперсию этой случайной величины.
Решение. Математическое ожидание: M[X] = λ = 0.004*5000 = 20. Дисперсия: D[X] = λ = 20
Закон распределения:
| X | 0 | 1 | 2 | … | m | … |
| P | e-20 | 20e-20 | 200e-20 | … | 20me-20/m! | … |
Пример №3. На телефонной станции неправильное соединение происходит с вероятностью 1/200. Найдите вероятность того, что среди 200 соединений произойдет:
а) ровно одно неправильное соединение;
б) меньше чем три неправильных соединения;
в) больше чем два неправильных соединения.
Решение. По условию задачи вероятность события мала, поэтому используем формулу Пуассона (15).
а) Задано: n = 200, p = 1/200, k = 1. Найдем P200(1).
Получаем: 
. Тогда P200(1) ≈ e-1≈ 0,3679.
б) Задано: n = 200, p = 1/200, k < 3. Найдем P200(k < 3).
Имеем: a = 1.
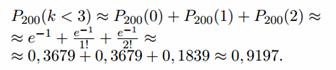
в) Задано: n = 200, p = 1/200, k > 2. Найдем P200(k > 2).
Эту задачу можно решить проще: найти вероятность противоположного события, так как в этом случае нужно вычислить меньше слагаемых. Принимая во внимание предыдущий случай, имеем
P200(k>2) = 1-P200(k≤2) = 1-P200(k<3) ≈ 1-0,9197 ≈ 0,0803
Рассмотрим случай, когда n является достаточно большим, а p — достаточно малым; положим np = a, где a — некоторое число. В этом случае искомая вероятность определяется формулой Пуассона:
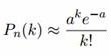
Вероятность появления k событий за время длительностью t можно также найти по формуле Пуассона:
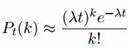
где λ — интенсивность потока событий, то есть среднее число событий, которые появляются в единицу времени.
Пример №4. Вероятность того, что деталь бракованная, равна 0.005. проверяется 400 деталей. Укажите формулу вычисления вероятности того, что больше 3 деталей оказались с браком.
Пример №5. Вероятность появления бракованных деталей при их массовом производстве равна p. определить вероятность того, что в партии из N деталей содержится а) ровно три детали; б) не более трех бракованных деталей.
p=0,001; N = 4500
Решение.
Вероятность р мала, а число n велико. np = 4.5 < 10. Значит случайная величина Х – распределена по Пуассоновскому распределению. Составим закон.
Случайная величина X имеет область значений (0,1,2,...,m). Вероятности этих значений можно найти по формуле:
Найдем ряд распределения X.
Здесь λ = np = 4500*0.001 = 4.5
P(0) = e- λ = e-4.5 = 0.01111
P(1) = λe-λ = 4.5e-4.5 = 0.04999
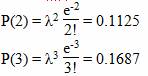
Тогда вероятность того, что в партии из N деталей содержится ровно три детали, равна:
Тогда вероятность того, что в партии из N деталей содержится не более трех бракованных деталей:
P(x<3) = P(0) + P(1) + P(2) = 0,01111 + 0,04999 + 0,1125 = 0,1736
Пример №6. Автоматическая телефонная станция получает в среднем за час N вызовов. Определить вероятность того, что за данную минуту она получит: а) ровно два вызова; б) более двух вызовов.
N = 18
Решение.
За одну минуту АТС в среднем получает λ = 18/60 мин. = 0,3
Считая, что случайное число X вызовов, поступивших на АТС за одну минуту,
подчиняется закону Пуассона, по формуле найдем искомую вероятность
Найдем ряд распределения X.
Здесь λ = 0.3
P(0) = e- λ = e-0.3 = 0.7408
P(1) = λe-λ = 0.3e-0.3 = 0.2222
Вероятность того, что за данную минуту она получит ровно два вызова:
P(2) = 0,03334
Вероятность того, что за данную минуту она получит более двух вызовов:
P(x>2) = 1 – 0,7408 – 0,2222 – 0,03334 = 0,00366
Пример №7. Рассматриваются два элемента, работающих независимо друг от друга. Продолжительность времени безотказной работы имеет показательное распределение с параметром λ1 = 0,02 для первого элемента и λ2 = 0,05 для второго элемента. Найти вероятность того, что за 10 часов: а) оба элемента будут работать безотказно; б) только Вероятность того, что за 10 часов элемент №1 не выйдет из строя:
Рещение.
P1(0) = e-λ1*t = e-0.02*10 = 0,8187
Вероятность того, что за 10 часов элемент №2 не выйдет из строя:
P2(0) = e-λ2*t = e-0.05*10 = 0,6065
а) оба элемента будут работать безотказно;
P(2) = P1(0)*P2(0) = 0,8187*0,6065 = 0,4966
б) только один элемент выйдет из строя.
P(1) = P1(0)*(1-P2(0)) + (1-P1(0))*P2(0) = 0.8187*(1-0.6065) + (1-0.8187)*0.6065 = 0.4321
Пример №7. Производство даёт 1% брака. Какова вероятность того, что из взятых на исследование 1100 изделий выбраковано будет не больше 17?
Примечание: поскольку здесь n*p=1100*0.01=11 > 10, то необходимо использовать теорему Лапласа.
