Геометрическое распределение
В геометрическом распределении опыты в схеме Бернулли проводятся до первого успеха, с вероятностью успеха р в единичном опыте.Примерами таких величин могут быть:
- число выстрелов до первого попадания;
- число испытаний прибора до первого отказа;
- число шаров до первого появления белого. см. решение;
- число бросаний монеты до первого выпадения решки и т.д.
| X | 1 | 2 | 3 | … | m | … |
| p | p | qp | q2p | … | qm-1p | … |
Математическое ожидание и дисперсия случайной величины Х, имеющей геометрическое распределение с параметром р, равны:
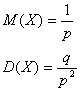
Гипергеометрическое распределение
Дискретная случайная величина имеет гипергеометрическое распределение с параметрами n, k, m, если она принимает значения 0, 1, 2, ... с вероятностями
.
Гипергеометрическое распределение имеет случайная величина Х, равная числу объектов, обладающих заданным свойством, среди m объектов, случайно извлеченных (без возврата) из совокупности n объектов, k из которых обладают этим свойством.
Например:
- В партии из 10 деталей 3 бракованных. Извлекается 4 детали. Х – число годных деталей среди извлеченных. (m = 4, n = 10, k = 3). см. решение
Математическое ожидание случайной величины Х, имеющей гипергеометрическое распределение, и ее дисперсия равны:
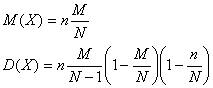
Пример №1. В урне 2 белых и 3 черных шара. Шары наудачу достают из урны без возвращения до тех пор, пока не появится белый шар. Как только это произойдет, процесс прекращается. Составить таблицу распределения случайной величины X – числа произведенных опытов, найти F(x), P(X ≤ 2), M(X), D(X).·
Решение: Обозначим через А – появление белого шара. Опыт может быть проведен только один раз, если белый шар появится сразу:
. Если же в первый раз белый шар не появился, а появился при втором извлечении, то X=2. Вероятность такого события равна 
. Аналогично: 
, 
, 
. Запишем данные в таблицу:
| X | 1 | 2 | 3 | 4 |
| P | 0,4 | 0,3 | 0,2 | 0,1 |
НайдемF(x):
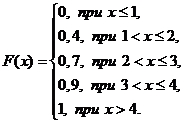
Найдем P(X ≤ 2) = P(X = 1 или X = 2) = 0,4 + 0,3 = 0,7
M(X) = 1 · 0,4 + 2 · 0,3 +3 · 0,2 + 4 · 0,1 = 2.
D(X) = (1-2)2 · 0,4 + (2-2)2 · 0,3 +(3-2)2 · 0,2 + (4-2)2 · 0,1 = 1.
Пример №2. В ящике содержится 11 деталей, среди которых 5 бракованных. Сборщик наудачу извлекает 4 деталей.
1. Найти вероятность того, что среди извлеченных деталей: a) 4 бракованных; b) одна бракованная; c) две бракованные; d) хотя бы одна бракованная.
2. Составить закон распределения случайной величины X– числа бракованных деталей среди извлеченных.
3. Найти M(X), D(X), σ(X).
4. Вычислить P(1<X<4)
Решение:
1. Найти вероятность того, что среди извлеченных деталей:
a) 4 бракованных;
b) одна бракованная;
Общее число возможных элементарных исходов для данных испытаний равно числу способов, которыми можно извлечь 4 детали из 11:
Подсчитаем число исходов, благоприятствующих данному событию (среди 4 деталей ровно 1 деталь дефектная):
Остальные 3 детали можно выбрать из 7:
Следовательно, число благоприятствующих исходов равно: 5*20 = 100
Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов: P(1) = 100/330 = 0,303
c) две бракованные;
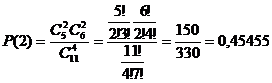
d) хотя бы одна бракованная.
Вероятность того, что нет дефектных деталей. X = 0.
Тогда вероятность того, что хотя бы одна бракованная составит:
P = 1 – P(0) = 1 – 0,0455 = 0,95
2. Составим закон распределения P(x), X -числа бракованных деталей среди извлеченных.
Найдем вероятность появления трех бракованных изделий.
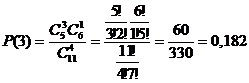
| X | 0 | 1 | 2 | 3 | 4 |
| P | 0,0455 | 0,303 | 0,4545 | 0,182 | 0,015 |
2. Найдем M(X), D(X), σ(X).
Математическое ожидание находим по формуле m = ∑xipi.
Математическое ожидание M[X].
M[x] = 0*0.0455 + 1*0.303 + 2*0.4545 + 3*0.182 + 4*0.015 = 1.818
Дисперсию находим по формуле d = ∑x2ipi - M[x]2.
Дисперсия D[X].
D[X] = 02*0.0455 + 12*0.303 + 22*0.4545 + 32*0.182 + 42*0.015 - 1.8182 = 0.694
Среднее квадратическое отклонение σ(x).
3. Вычислим P(1<X<4). Для этого найдем функцию распределения F(X).
F(x≤0) = 0
F(0< x ≤1) = 0.0455
F(1< x ≤2) = 0.303 + 0.0455 = 0.349
F(2< x ≤3) = 0.455 + 0.349 = 0.803
F(3< x ≤4) = 0.182 + 0.803 = 0.985
F(x>4) = 1
Вероятность попадания СВ в тот ли иной интервал находится по формуле:
P(a ≤ X < b) = F(b) - F(a)
Найдем вероятность того, что СВ будет находиться в интервале 1 ≤ X < 4
P(1 ≤ X < 4) = F(4) - F(1) = 0.985 - 0.0455 = 0.9395
Пример №3. В партии 7 деталей 3 бракованные. Контролер наудачу достает 4 детали. Составить закон распределения случайной величины Х – числа годных деталей в выборке. Найти математическое ожидание и дисперсию Х. Построить график функции распределения.
Всего исправных деталей: 7-3 = 4
1. Найдем вероятность того, что среди выбранных 4 деталей одна исправная.
Общее число возможных элементарных исходов для данных испытаний равно числу способов, которыми можно извлечь 4 детали из 7:
Подсчитаем число исходов, благоприятствующих данному событию:
а) одну деталь среди 4 годных можно выбрать способами, количество которых равно:
б) Остальные 3 бракованные детали можно выбрать из 3 бракованных:
Аналогично:
2. Найдем вероятность того, что среди выбранных 4 деталей 2 исправных.
3. Найдем вероятность того, что среди выбранных 4 деталей 3 исправных.
4. Найдем вероятность того, что все выбранные детали годные.
| x | 1 | 2 | 3 | 4 |
| p | 0.114 | 0.514 | 0.343 | 0.029 |
Математическое ожидание M[X].
M[x] = 1*0.114 + 2*0.514 + 3*0.343 + 4*0.029 = 2.287
Дисперсию находим по формуле d = ∑x2ipi - M[x]2.
Дисперсия D[X].
D[X] = 12*0.114 + 22*0.514 + 32*0.343 + 42*0.029 - 2.2872 = 0.491
Среднее квадратическое отклонение σ(x).
