Проекция вектора
Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:|a| - модуль вектора a.
Классификация проекций вектора
Виды проекций по определению проекция вектора
- Геометрическая проекция вектора AB на ось (вектор) называется вектор A'B', начало которого A’ есть проекция начала A на ось (вектор), а конец B’ – проекция конца B на ту же ось.
- Алгебраическая проекция вектора AB на ось (вектор) называется длина вектора A'B', взятая со знаком + или -, в зависимости от того, имеет ли вектор A'B' то же направление, что и ось (вектор).
Виды проекций по системе координат
- проекции на плоскости (система координат OX,OY). Пример: a(2;-3), a=2i-3j
- проекции в пространстве (система координат OX,OY, OZ). Пример: a(2;-3;1), a=2i-3j+k

- проекции в N-мерном пространстве
Свойства проекции вектора
- Геометрическая проекция вектора есть вектор (имеет направление).
- Алгебраическая проекция вектора есть число.
Теоремы о проекциях вектора
Теорема 1. Проекция суммы векторов на какую-либо ось равна проекции слагаемых векторов на ту же ось.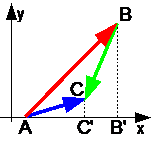 AC'=AB'+B'C'
AC'=AB'+B'C'
Теорема 2. Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:
Виды проекций вектора
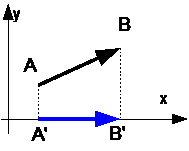
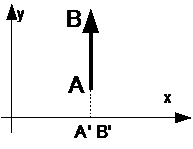
- проекция на ось OX.
- проекция на ось OY.
- проекция на вектор.
| Проекция на ось OX | Проекция на ось OY | Проекция на вектор |
Если направление вектора A’B’ совпадает с направлением оси OX, то проекция вектора A’B’ имеет положительный знак.
| Если направление вектора A’B’ совпадает с направлением оси OY, то проекция вектора A’B’ имеет положительный знак.
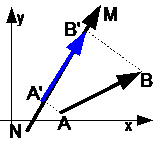
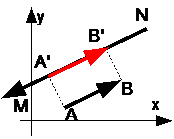
| Если направление вектора A’B’ совпадает с направлением вектора NM, то проекция вектора A’B’ имеет положительный знак.
|
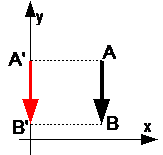
Если направление вектора противоположно с направлением оси OX, то проекция вектора A’B’ имеет отрицательный знак.
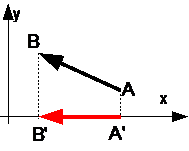
| Если направление вектора A’B’ противоположно с направлением оси OY, то проекция вектора A’B’ имеет отрицательный знак.

| Если направление вектора A’B’ противоположно с направлением вектора NM, то проекция вектора A’B’ имеет отрицательный знак.

|
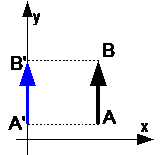
Если вектор AB параллелен оси OX, то проекция вектора A’B’ равна модулю вектора AB.
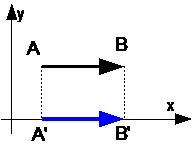
| Если вектор AB параллелен оси OY, то проекция вектора A’B’ равна модулю вектора AB.
| Если вектор AB параллелен вектору NM, то проекция вектора A’B’ равна модулю вектора AB.

|
Если вектор AB перпендикулярен оси OX, то проекция A’B’ равна нулю (нуль-вектор).
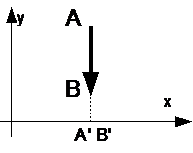
| Если вектор AB перпендикулярен оси OY, то проекция A’B’ равна нулю (нуль-вектор).
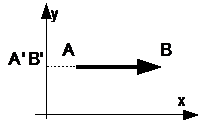
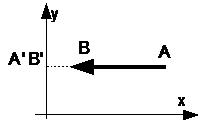
| Если вектор AB перпендикулярен вектору NM, то проекция A’B’ равна нулю (нуль-вектор).
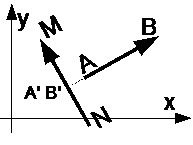
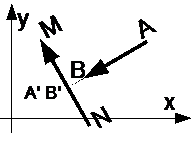
|
1. Вопрос: Может ли проекция вектора иметь отрицательный знак. Ответ: Да, проекций вектора может быть отрицательной величиной. В этом случае, вектор имеет противоположное направление (см. как направлены ось OX и вектор AB)
2. Вопрос: Может ли проекция вектора совпадать с модулем вектора. Ответ: Да, может. В этом случае, векторы параллельны (или лежат на одной прямой).
3. Вопрос: Может ли проекция вектора быть равна нулю (нуль-вектор). Ответ: Да, может. В этом случае вектор перпендикулярен соответствующей оси (вектору).
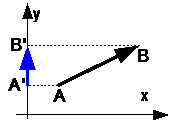
Пример 1. Вектор ![]() (рис. 1) образует с осью OX (она задана вектором a) угол 60о. Если OE есть единица масштаба, то |b|=4, так что
(рис. 1) образует с осью OX (она задана вектором a) угол 60о. Если OE есть единица масштаба, то |b|=4, так что ![]() .
.
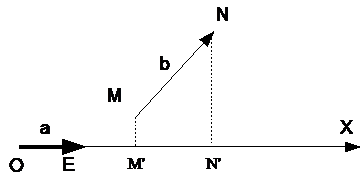
Действительно, длина вектора ![]() (геометрической проекции b) равна 2, а направление совпадает с направлением оси OX.
(геометрической проекции b) равна 2, а направление совпадает с направлением оси OX.
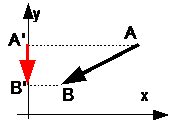
Пример 2. Вектор ![]() (рис. 2) образует с осью OX (с вектором a) угол (a,b) = 120o. Длина |b| вектора b равна 4, поэтому прab=4·cos120o = -2.
(рис. 2) образует с осью OX (с вектором a) угол (a,b) = 120o. Длина |b| вектора b равна 4, поэтому прab=4·cos120o = -2.
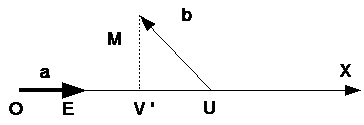
Действительно, длина вектора ![]() равна 2, а направление противоположно направлению оси.
равна 2, а направление противоположно направлению оси.
Пример 3. Пусть вектор b задан через координаты точек M(1;1), N(4;5).

Координаты вектора: MN(4-1;5-1) = MN(3;4)
Тогда модуль вектора MN равен:
![]()
Направляющий вектор для оси OX равен вектору M’N’, где координаты точек M’(1;0) N’(4;0). Следовательно, вектор M’N’ имеет координаты: x = 4-1, y = 0-0 = 0.
M’N’(3;0)
![]()
Пример 4. Найти проекцию вектора c на вектор d;
с = АС = (-2;-1;3), d = CB(-5;-3;3)
![]()
Найдем проекцию вектора AC на вектор BC
![]()
![]()
Пример 5. Найти проекцию прb(-2a+4b)
где a=2m+3n и b=4m-n, |m|=k, |n|=l, угол между ∠(m,n)= π
Тогда -2a+4b = -4m+6n + 16m-4n = 12m+2n

а) Рассмотрим треугольник со сторонами a,b,c. По теореме косинусов:
a2 = b2 + c2 – 2bc∙cos(b,c), откуда
или
Поскольку угол между векторами π, т.е. 180о, то векторы лежат на одной оси.
Таким образом, 4m-n = 4*1 – 1 = 3.
Находим проекцию.

