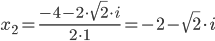Дискриминант
Квадратичная функция имеет вид:ax2+bx+c=0
Формула дискриминанта:
D=b2-4ac
Онлайн-калькулятор предназначен для нахождения дискриминанта и корней функции для уравнений вида: ax2+bx+c=0.
см. также как выделить полный квадрат и как построить параболу ax2+bx+c=0.
Виды дискриминантов
Формула дискриминанта зависит от степени многочленаanxn + an-1xn-1 + ... + a1x + a0 = 0.
Свойства дискриминанта
- Дискриминант равен 0, когда многочлен имеет кратные корни (равные корни).
- Дискриминант является симметрическим многочленом относительно корней многочлена и поэтому является многочленом от его коэффициентов; более того, коэффициенты этого многочлена целые независимо от расширения, в котором берутся корни.
Классификация дискриминантов
| D>0 | D=0 | D<0 |
При D > 0 корней — два. Формула для вычислений:
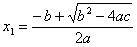
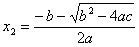
|
при D = 0 корень один кратности 2 (корни равны). Формула для вычислений:
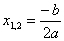 |
при D < 0 вещественных корней нет. Существуют два комплексных корня. Формула для вычислений:
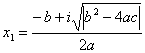
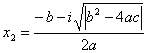
|
| При a > 0, x1 < x2. При a < 0, x1 > x2
Что означает, если дискриминант больше нуля: значит существуют вещественные корни, график квадратичной функции пересекает ось Х в двух местах. |
x1 = x2 = -b/2a
Что означает, если дискриминант равен нулю: значит существует один вещественный корень, график функции пересекает ось Х в одном месте. |
Что означает, если дискриминант меньше нуля: значит не существует вещественных корней, а только комплексные корни. График функции не пересекает ось Х.
|

 |

 |

 |
Пример расчета для дискриминанта больше нуля
2x2+3x+1=0
Находим дискриминант: D=32-4·2·1=1
Корни уравнения: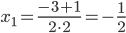 ;
; 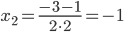
2x2+3x+1=0
Находим дискриминант: D=32-4·2·1=1
Корни уравнения:
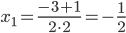 ;
; 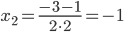
Пример расчета для дискриминанта равного нулю
9/4x2+3x+1=0
Находим дискриминант: D=32-4·9/4·1=0
Корни уравнения: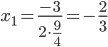
9/4x2+3x+1=0
Находим дискриминант: D=32-4·9/4·1=0
Корни уравнения:
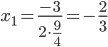
Пример расчета для дискриминанта меньше нуля
x2 +4 x + 6 = 0
Находим дискриминант:
Корни уравнения:
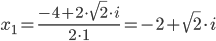 ,
, 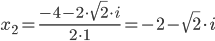
x2 +4 x + 6 = 0
Находим дискриминант:
D=42 - 4·1·6=-8
Корни уравнения:
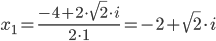 ,
,