Площадь треугольника
Пусть точки A1(x1; y1), A2(x2; y2), A3(x3; y3) - вершины треугольника, тогда его площадь выражается формулой: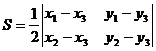
В правой части стоит определитель второго порядка. Площадь треугольника всегда положительна.
Примечание: если определитель равен 0, то это означает, что точки лежат на одной прямой. Таким образом, равенство нулю определителя задает условие, при котором три точки лежат на одной прямой.
Инструкция. Для нахождения площади треугольника заполните координаты вершин, нажмите Далее. Полученное решение сохраняется в файле Word.
Пример. Найти площадь треугольника с вершинами A(1,3), B(2,-5), C(-8,4)
Решение. Принимая A за первую вершину, находим:
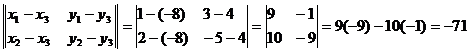
S=
1
2
·|-71|
= 35.5
Произвольный треугольник
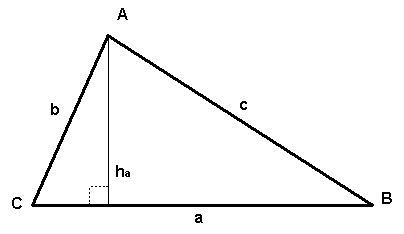
a,b,c – длины сторон треугольника,
p =(a+b+c)/2 – полупериметр,
ha – высота треугольника
S = ½∙a∙ha
S = ½∙a∙b∙sinC
Формула Герона
Площадь треугольника через радиус
R и r – радиусы вписанной и описанной окружностейS = p∙r; S = a∙b∙c/(4R)
Прямоугольный треугольник
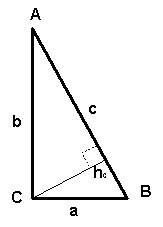
a и b – катеты; c - гипотенуза
S = ½∙a∙b
S = ½∙c∙hc
S = ½∙c∙hc
Равносторонний треугольник