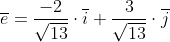Длина отрезка на плоскости

Длина вектора (норма вектора). Расстояние между двумя точками на плоскости.
Длина радиуса-вектора a=(x;y) находится по формуле:

Длина вектора a=AB=(x_B-x_A;y_B-y_A) находится по формуле:

и определяет норму вектора. С помощью этой формулы вычисляется также расстояние между двумя точками на плоскости:

Инструкция. Для онлайн решения соответствующих задач введите коэффициенты при переменных и нажмите кнопку Решение.

Пример №1. Найти длину вектора AB, если A(¹/₂;-1) и B(0;4).
Решение
Длина вектора находится по формуле:
$|AB|=\sqrt{(x_{B}-x_{A})^{2}+(y_{B}-y_{A})^{2}}$
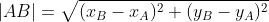
По формуле находим:
$|AB|=\sqrt{(0-{1 \over 2})^{2}+(4-(-1))^{2}}=\sqrt{{101 \over 4}}$

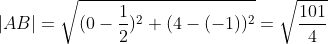
Пример №2. Найти единичный вектор того же направления, что и вектор a(-2;3).
Решение
Находим длину данного вектора:
$|a|=\sqrt{-2^{2}+3^{2}}=\sqrt{13}$
Единичный вектор e того же направления, что и вектор a, равен:
$e=\frac{a}{|a|}=\frac{a}{\sqrt{13}}$
Каждая проекция вектора e также в |a| раз меньше соответствующей проекции вектора a, поэтому:
$\overline{e}=\frac{-2}{\sqrt{13}}\cdot \overline{i}+\frac{3}{\sqrt{13}}\cdot \overline{j}$

Длина отрезка на плоскости

Правила ввода данных

Поиск

Процесс

Сообщение