Объем параллелепипеда
Объем параллелепипеда, построенного на векторах a1(X1;Y1;Z1), a2(X2;Y2;Z2), a3(X3;Y3;Z3) равен: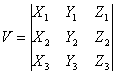
Инструкция. Заполните координаты векторов или координаты вершин, нажмите Далее. Результат решение сохраняется в формате Word.
или
Пример 1. Даны координаты параллелепипеда: A1(0,9,7), A2(1/2,-3,1), A3(-3,1,2), A4(4,2,0). Найти объем параллелепипеда.
Находим координаты векторов. Например, для вектора A1A2.
X = x2 - x1; Y = y2 - y1; Z = z2 - z1
X = 1/2-0 = 1/2; Y = (-3)-9 = -12; Z = 1-7 = -6
A1A2(1/2;-12;-6)
A1A3(-3;-8;-5)
A1A4(4;-7;-7)
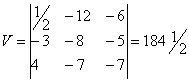
∆ = 1/2·((-8) · (-7) - (-7) · (-5)) – (-3) · ((-12) · (-7) - (-7)· (-6)) + 4· ((-12) · (-5) - (-8) · (-6)) = 1841/2
Пример 2. Найти объем параллелепипеда, построенного на векторах: a1(1,2,1), a2(-1,3,2), A3(0,4,8)
Объем параллелепипеда, построенного на векторах a1(X1;Y1;Z1), a2(X2;Y2;Z2), a3(X3;Y3;Z3) равен:
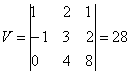
Где (28) нашли как определитель матрицы: ∆ = 1· (3·8 - 4·2) – (-1) · (2·8 - 4·1) + 0 = 28

