Объем пирамиды
Объем пирамиды, построенной на векторах a1(X1;Y1;Z1), a2(X2;Y2;Z2), a3(X3;Y3;Z3) равен: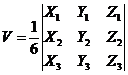
Если заданы координаты точек вершин пирамиды, то координаты векторов находятся по формуле:
X = xj - xi; Y = yj - yi; Z = zj - zi
где xi, yi, zi - координаты точки Аi; xj, yj, zj - координаты точки Аj;
Инструкция. Заполните координаты вершин, нажмите Далее. Полученное решение сохраняется в файле MS Word.
или
Пример №1. Даны координаты пирамиды: A1(2,-1,1), A2(5,5,4), A3(3,2,-1), A4(4,1,3). Найти объем пирамиды A1A2A3A4.
Вектора A1A2: X = x2 - x1; Y = y2 - y1; Z = z2 - z1
X = 5-2 = 3; Y = 5-(-1) = 6; Z = 4-1 = 3
По формуле находим остальные координаты векторов:
A1A2(3;6;3)
A1A3(1;3;-2)
A1A4(2;2;2)
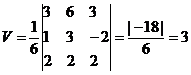
∆ = 3·(3·2 - 2·(-2)) - 1·(6·2 - 2·3) + 2·(6· (-2) - 3·3) = -18
Пример №2. Найти объем пирамиды, отсекаемой от угла плоскостью, проходящей через точки А(0,2,-1), В(3,4,2), С(-3,0,4).

