Множество точек на плоскости
Уравнению с переменными x и y соответствует на плоскости некоторая линия как множество точек, координаты которых удовлетворяют этому уравнению. Обратно: линия на плоскости, представляющей множество точек, соответствует некоторое уравнение с переменными x и y.
Пример №1. Составить уравнение множества точек на плоскости, равноудаленных от точек A(1;2) и B(-2;0).
Решение
Пусть точка М принадлежит искомому множеству точек, тогда МА=МВ. Так как
![]()
![]()
то
![]()
После возведения левой и правой частей в квадрат и упрощений получим:
(x-1)2 + (y-2)2 = (x + 2)2 + y2
x2 - 2x + 1 + y2 - 4y + 4 = x2 + 4x + 4 + y2
или
- 6x - 4y + 1 = 0
Ответ: - 6x - 4y + 1 = 0.
Пример №2.
Составить уравнение множества точек на плоскости, отношение расстояний которых от точки A(1;-2) и от прямой x=1 равно 1/2.
Решение
Из условия следует, что для любой точки M(x;y) искомого множества справедливо соотношение MA:MB = 1/2. Так как:
![]()
![]()
то
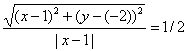
или
![]()
Возведя левую и правую части в квадрат и упрощая, получим:
4(x - 1)2 + 4(y + 2)2 = |x - 1|2
т.е.
4(x2 - 2x + 1) + 4(y2 + 4y + 4) = x2 - 2x + 1
или
3x2 + 4y2 - 6x +16y +19 = 0
Ответ: 3x2 + 4y2 - 6x +16y +19 = 0.
Пример №3. Составить уравнение линий, если расстояние каждой ее точки А(2,0) относится к расстоянию до прямой 5x+8=0 как 5:4.
Решение. Выражаем x = -8/5. λ=5/4. Подставляем данные в задание №2.
Пример №4. Составить уравнение линии, каждая точка которой равноудалена от прямой x+6=0 и от начала координат.
Примечание. Здесь x=-6, λ=1.
см. также как построить параболу, гиперболу, эллипс, окружность.