Внутренние углы треугольника
Внутренние углы треугольника с вершинами A, B, C находятся по формуле:Известно, что если в треугольнике квадрат большей стороны больше суммы квадратов двух других сторон, то этот треугольник тупоугольный. Например, если AB2 > BC2 + AC2, то сторона AB лежит против тупого угла.
Пример
Дан треугольник A(-1;-1), B(3;2), C(5;0).
Находим угловые коэффициенты сторон этого треугольника:



Найдем углы треугольника:
Угол A
Угол φ между двумя прямыми, заданными уравнениями с угловыми коэффициентами y = k1x + b1 и y2 = k2x + b2, вычисляется по формуле:

Угловые коэффициенты данных прямых равны 3/4 и 1/6. Воспользуемся формулой, причем ее правую часть берем по модулю:


Угол B. Угловые коэффициенты данных прямых равны -1 и 3/4.



Складывая найденные значения углов, получаем 27.41+81.87+54.46 = 163.74. Сумма углов треугольника оказалась меньше 1800 потому, что при вычислении был найден не внутренний угол треугольника, а внешний, смежный с ним. Известно, что если в треугольнике квадрат большей стороны больше суммы квадратов двух других сторон, то этот треугольник тупоугольный.
Поскольку угол B тупой, то B = 1800 - 81.870 = 98.130





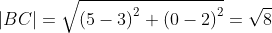
Теорема косинусов
Для угла A:

Для угла B:

 =
=Для угла C:

Теорема синусов
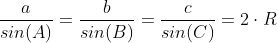
R - радиус вписанной окружности.


