Угол между векторами
Угол между векторами a(x1;y1;z1) и b(x2;y2;z2) вычисляется по формуле: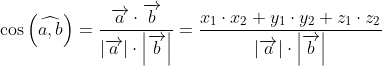
Инструкция. Заполните координаты векторов и нажмите кнопку Решение.
Пример 1. Найти скалярное произведение векторов a=(-2;3;1) и b(0;-1;5).
Решение. Скалярное произведение векторов a и b, заданных своими координатам, находится по формуле: a•b = x1•x2 + y1•y2 + c1•c2. По формуле находим:
(-2)•0 + 3•(-1) + 1•5 = 2
Пример 2. Даны векторы a и b. С помощью скалярного произведения векторов найти угол между этими векторами (в угловых градусах или радианах) и проекцию вектора c=2a+b на вектор d=a-3b. Сделать схематические рисунки.
a=(-1;2;6), b=(7;-7;6)
Решение.
c=2a+b = 2(-1;2;6) + (7;-7;6) = (-2+7;4-7;12+6) = (5;-3;18)
d=a-3b = (-1;2;6) - 3(7;-7;6) = (-1-21; 2+21; 6-18) = (-22;23;-12)
Найдем скалярное произведение векторов a=(5;-3;18) и b(-22;23;-12).
По формуле находим:
a*b = 5*(-22) + (-3)*23 + 18*(-12) = -395
Найдем модуль вектора a.
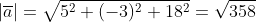
Найдем модуль вектора b.
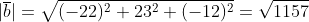
Найдем угол между векторами:
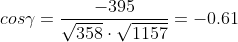
γ = arccos(-0.61) = 127.86o

