Уравнение параллельной прямой
Прямая, проходящая через точку K(x0; y0) и параллельная прямойy = kx + a находится по формуле:
Альтернативная формула:
Прямая, проходящая через точку M1(x1; y1) и параллельная прямой Ax+By+C=0, представляется уравнением
назначение сервиса. Онлайн-калькулятор предназначен для составления уравнения параллельной прямой (см. также как составить уравнение перпендикулярной прямой).
а) параллельно прямой 2x+3y -7 = 0;
б) перпендикулярно прямой 2x+3y -7 = 0.
Решение. Представим уравнение с угловым коэффициентом в виде
y = kx + a. Для этого перенесем все значения кроме y в правую часть: 3y = -2x + 7. Затем разделим правую часть на коэффициент 3. Получим: y = -2/3x + 7/3
Найдем уравнение NK, проходящее через точку K(-2;1), параллельно прямой y = -2/3x + 7/3
Подставляя x0 = -2, k = -2/3, y0 = 1 получим:
y-1 = -2/3(x-(-2))
или
y = -2/3x - 1/3 или 3y + 2x +1 = 0
Пример №2. Написать уравнение прямой, параллельной прямой 2x + 5y = 0 и образующей вместе с осями координат треугольник, площадь которого равна 5.
Решение. Так как прямые параллельны, то уравнение искомой прямой 2x + 5y + C = 0. Площадь прямоугольного треугольника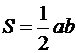 
, где a и b его катеты. Найдем точки пересечения искомой прямой с осями координат:
;
.
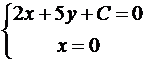
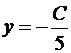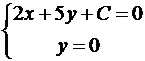
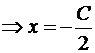Итак, A(-C/2,0), B(0,-C/5). Подставим в формулу для площади: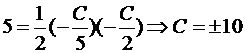 
. Получаем два решения: 2x + 5y + 10 = 0 и 2x + 5y – 10 = 0.
Пример №3. Составить уравнение прямой, проходящей через точку (-2; 5) и параллельной прямой Пример №4. Решив пример 3 (A=5, B=-7) по формуле (2), найдем 5(x+2)-7(y-5)=0.
Пример №5. Составить уравнение прямой, проходящей через точку (-2;5) и параллельной прямой 7x+10=0.
5x-7y-4=0.
Решение. Данную прямую можно представить уравнением y = 5/7x – 4/7 (здесь a = 5/7). Уравнение искомой прямой есть y – 5 = 5/7(x – (-2)), т.е. 7(y-5)=5(x+2) или 5x-7y+45=0.
Решение. Здесь A=7, B=0. Формула (2) дает 7(x+2)=0, т.е. x+2=0. Формула (1) неприменима, так как данное уравнение нельзя разрешить относительно y (данная прямая параллельна оси ординат).
