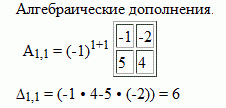Как найти общее и частное решение системы линейных уравнений
Пример 1. Найти общее решение и какое–нибудь частное решение системы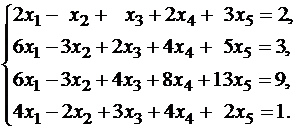
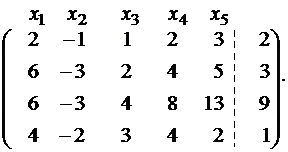
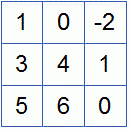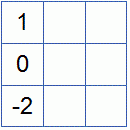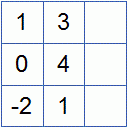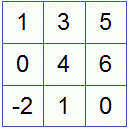
Пунктиром отделена основная матрица A. Сверху пишем неизвестные системы, имея в виду возможную перестановку слагаемых в уравнениях системы. Определяя ранг расширенной матрицы, одновременно найдем ранг и основной. В матрице B первый и второй столбцы пропорциональны. Из двух пропорциональных столбцов в базисный минор может попасть только один, поэтому перенесем, например, первый столбец за пунктирную черту с обратным знаком. Для системы это означает перенос членов с x1 в правую часть уравнений.

Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы. Работаем с первой строкой: умножим первую строку матрицы на (-3) и прибавим ко второй и третьей строкам по очереди. Затем первую строку умножим на (-2) и прибавим к четвертой.
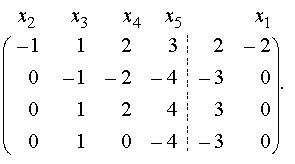
Вторая и третья строки пропорциональны, следовательно, одну из них, например вторую, можно вычеркнуть. Это равносильно вычеркиванию второго уравнения системы, так как оно является следствием третьего.
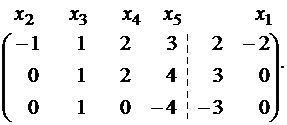
Теперь работаем со второй строкой: умножим ее на (-1) и прибавим к третьей.
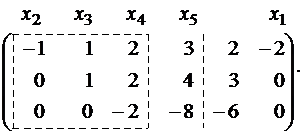
Минор, обведенный пунктиром, имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на главной диагонали), причем этот минор принадлежит как основной матрице, так и расширенной, следовательно rangA = rangB = 3.
Минор
 является базисным. В него вошли коэффициенты при неизвестных x2, x3, x4, значит, неизвестные x2, x3, x4 – зависимые, а x1, x5 – свободные.
является базисным. В него вошли коэффициенты при неизвестных x2, x3, x4, значит, неизвестные x2, x3, x4 – зависимые, а x1, x5 – свободные.
Преобразуем матрицу, оставляя слева только базисный минор (что соответствует пункту 4 приведенного выше алгоритма решения).
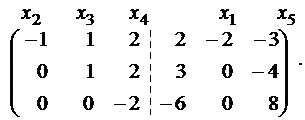
Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид
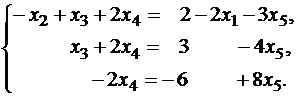
x4=3-4x5, x3=3-4x5-2x4=3-4x5-6+8x5=-3+4x5
x2=x3+2x4-2+2x1+3x5 = -3+4x5+6-8x5-2+2x1+3x5 = 1+2x1-x5
Получили соотношения, выражающие зависимые переменные x2, x3, x4 через свободные x1 и x5, то есть нашли общее решение:
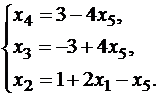
Придавая свободным неизвестным любые значения, получим сколько угодно частных решений. Найдем два частных решения:
1) пусть x1 = x5 = 0, тогда x2 = 1, x3 = -3, x4 = 3;
2) положим x1 = 1, x5 = -1, тогда x2 = 4, x3 = -7, x4 = 7.
Таким образом, нашли два решения: (0,1,-3,3,0) – одно решение, (1,4,-7,7,-1) – другое решение.
Пример 2. Исследовать совместность, найти общее и одно частное решение системы
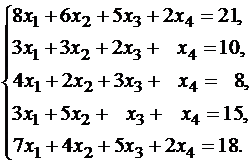
Решение. Переставим первое и второе уравнения, чтобы иметь единицу в первом уравнении и запишем матрицу B.
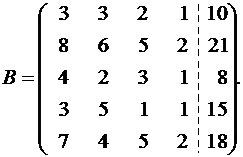
Получим нули в четвертом столбце, оперируя первой строкой:
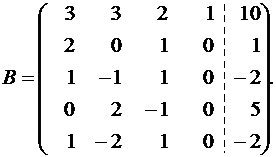
Теперь получим нули в третьем столбце с помощью второй строки:
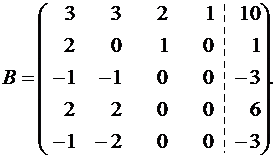
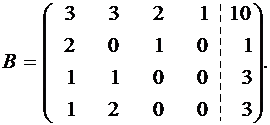 Третья и четвертая строки пропорциональны, поэтому одну из них можно вычеркнуть, не меняя ранга:
Третья и четвертая строки пропорциональны, поэтому одну из них можно вычеркнуть, не меняя ранга:
Третью строку умножим на (–2) и прибавим к четвертой:
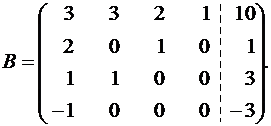
Видим, что ранги основной и расширенной матриц равны 4, причем ранг совпадает с числом неизвестных, следовательно, система имеет единственное решение:
-x1=-3 → x1=3; x2=3-x1 → x2=0; x3=1-2x1 → x3=5.
x4 = 10- 3x1 – 3x2 – 2x3 = 11.
Пример 3. Исследовать систему на совместность и найти решение, если оно существует.
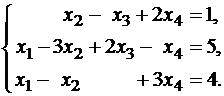
Решение. Составляем расширенную матрицу системы.
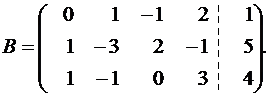
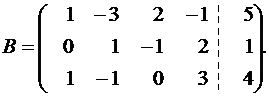 Переставляем первые два уравнения, чтобы в левом верхнем углу была 1:
Переставляем первые два уравнения, чтобы в левом верхнем углу была 1:
Умножая первую строку на (-1), складываем ее с третьей:
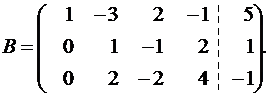
Умножим вторую строку на (-2) и прибавим к третьей:
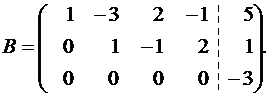
Система несовместна, так как в основной матрице получили строку, состоящую из нулей, которая вычеркивается при нахождении ранга, а в расширенной матрице последняя строка останется, то есть rB > rA.
Задание. Исследовать данную систему уравнений на совместность и решить ее средствами матричного исчисления.
Решение
Пример. Доказать совместимость системы линейных уравнений и решить ее двумя способами: 1) методом Гаусса; 2) методом Крамера. (ответ ввести в виде: x1,x2,x3)
Решение:doc:doc:xls
Ответ: 2,-1,3.
Пример. Дана система линейных уравнений. Доказать ее совместность. Найти общее решение системы и одно частное решение.
Решение
Ответ:x3 = - 1 + x4 + x5; x2 = 1 - x4; x1 = 2 + x4 - 3x5
Задание. Найти общее и частное решения каждой системы.
Решение.
Исследуем эту систему по теореме Кронекера-Капелли.
Выпишем расширенную и основную матрицы:
| 1 | 1 | 14 | 0 | 2 | 0 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
| x1 | x2 | x3 | x4 | x5 |
Здесь матрица А выделена жирным шрифтом.
Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
Умножим 1-ую строку на (3). Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:
| 0 | -1 | 40 | -3 | 6 | -1 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Умножим 2-ую строку на (2). Умножим 3-ую строку на (-3). Добавим 3-ую строку к 2-ой:
| 0 | -1 | 40 | -3 | 6 | -1 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), причем этот минор принадлежит как основной матрице, так и расширенной, следовательно rang(A) = rang(B) = 3. Поскольку ранг основной матрицы равен рангу расширенной, то система является совместной.
Этот минор является базисным. В него вошли коэффициенты при неизвестных x1,x2,x3, значит, неизвестные x1,x2,x3 – зависимые (базисные), а x4,x5 – свободные.
Преобразуем матрицу, оставляя слева только базисный минор.
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -1 | 3 | -6 |
| 2 | 3 | -3 | 1 | -3 | 2 |
| x1 | x2 | x3 | x4 | x5 |
27x3 =
- x2 + 13x3 = - 1 + 3x4 - 6x5
2x1 + 3x2 - 3x3 = 1 - 3x4 + 2x5
Методом исключения неизвестных находим:
Получили соотношения, выражающие зависимые переменные x1,x2,x3 через свободные x4,x5, то есть нашли общее решение:
x3 = 0
x2 = 1 - 3x4 + 6x5
x1 = - 1 + 3x4 - 8x5
Придавая свободным неизвестным любые значения, получим сколько угодно частных решений. Система является неопределенной, т.к. имеет более одного решения.
Задание. Решить систему уравнений.
Ответ:x2 = 2 - 1.67x3 + 0.67x4
x1 = 5 - 3.67x3 + 0.67x4
Придавая свободным неизвестным любые значения, получим сколько угодно частных решений. Система является неопределенной
Пример. Проверить совместность линейной системы уравнений и в случае совместности решить ее: а) по формулам Крамера; б) методом Гаусса.
Решение: Проверяем совместность системы с помощью теоремы Кронекера - Капелли. Согласно теореме Кронекера - Капелли, из того, что следует несовместность исходной системы.
Ответ: система не совместна.
Решение