Метод Гаусса

Определение метода Гаусса

Пусть дана система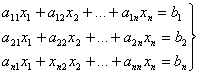

, ∆≠0. (1)
Метод Гаусса – это метод последовательного исключения неизвестных.

Суть метода Гаусса состоит в преобразовании (1) к системе с треугольной матрицей, из которой затем последовательно (обратным ходом) получаются значения всех неизвестных.

Вычислительные схемы

Схема единственного деления.
Схема последовательного алгоритма. На первом шаге метода среди элементов a_ij определяют максимальный по модулю элемент. Первое уравнение системы и уравнение с номером i₁ меняют местами. Далее стандартным образом производят исключение неизвестного x_i1 из всех уравнений, кроме первого.

Схема единственного деления

Пусть a₁₁≠0 (ведущий элемент) разделим на a₁₁ первое уравнение. Получим
x₁+a⁽¹⁾₁₂·x₂+...+a⁽¹⁾_1n·x_n=b⁽¹⁾₁ (2)
Пользуясь уравнением (2), легко исключить неизвестные x₁ из остальных уравнений системы (для этого достаточно из каждого уравнения вычесть уравнение (2) предварительно умноженное на соответствующий коэффициент при x₁), то есть на первом шаге получим
$формула Гаусса$ .
Иными словами, на 1 шаге каждый элемент последующих строк, начиная со второй, равен разности между исходным элементом и произведением его «проекции» на первый столбец и первую (преобразованную) строку.
Вслед за этим оставив первое уравнение в покое, над остальными уравнениями системы, полученной на первом шаге, совершим аналогичное преобразование: выберем из их числа уравнение с ведущим элементом и исключим с его помощью из остальных уравнений x₂ (шаг 2).
После n шагов вместо (1) получим равносильную систему

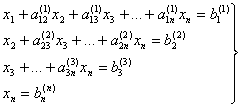(3)
Таким образом, на первом этапе мы получим треугольную систему (3). Этот этап называется прямым ходом.
На втором этапе (обратный ход) мы находим последовательно из (3) значения x_n , x_n_-1, …, x₁.
Обозначим полученное решение за x₀. Тогда разность ε=b-A·x₀ называется невязкой.
Если ε=0, то найденное решение x₀ является верным.

Вычисления по методу Гаусса выполняются в два этапа:

Первый этап называется прямым ходом метода. На первом этапе исходную систему преобразуют к треугольному виду.
Второй этап называется обратным ходом. На втором этапе решают треугольную систему, эквивалентную исходной.

Коэффициенты а₁₁, а₂₂, …, называют ведущими элементами.
На каждом шаге предполагалось, что ведущий элемент отличен от нуля. Если это не так, то в качестве ведущего можно использовать любой другой элемент, как бы переставив уравнения системы.

Назначение метода Гаусса

Метод Гаусса предназначен для решения систем линейных уравнений. Относится к прямым методам решения.

Виды метода Гаусса

Классический метод Гаусса;
Модификации метода Гаусса. Одной из модификаций метода Гаусса является схема с выбором главного элемента. Особенностью метода Гаусса с выбором главного элемента является такая перестановка уравнений, чтобы на k-ом шаге ведущим элементом оказывался наибольший по модулю элемент k-го столбца.
Метод Жордано-Гаусса;

Отличие метода Жордано-Гаусса от классического метода Гаусса состоит в применении правила прямоугольника, когда направление поиска решения происходит по главной диагонали (преобразование к единичной матрице). В методе Гаусса направление поиска решения происходит по столбцам (преобразование к системе с треугольной матрицей).
Проиллюстрируем отличие метода Жордано-Гаусса от метода Гаусса на примерах.

Пример решения методом Гаусса
Решим систему:

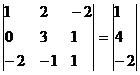
Для удобства вычислений поменяем строки местами:

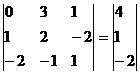
Умножим 2-ую строку на (2). Добавим 3-ую строку к 2-ой

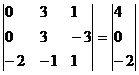
Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой

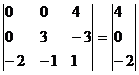
Из 1-ой строки выражаем x₃: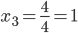
Из 2-ой строки выражаем x₂: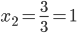
Из 3-ой строки выражаем x₁: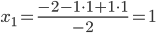

Пример решения методом Жордано-Гаусса
Эту же СЛАУ решим методом Жордано-Гаусса.

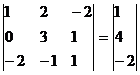
Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.
Разрешающий элемент равен (1).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
НЭ = СЭ - (А*В)/РЭ
РЭ - разрешающий элемент (1), А и В - элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.
Представим расчет каждого элемента в виде таблицы:

x₁	x₂	x₃	B
1 / 1 = 1	2 / 1 = 2	-2 / 1 = -2	1 / 1 = 1

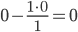
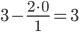
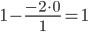
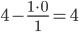
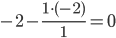
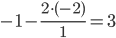
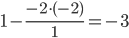
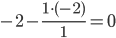
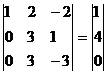
Разрешающий элемент равен (3).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
Представим расчет каждого элемента в виде таблицы:

x₁	x₂	x₃	B

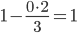
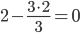
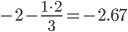
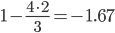
0 / 3 = 0	3 / 3 = 1	1 / 3 = 0.33	4 / 3 = 1.33

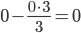
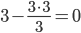
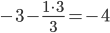
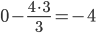
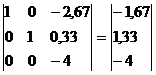
Разрешающий элемент равен (-4).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
Представим расчет каждого элемента в виде таблицы:

x₁	x₂	x₃	B


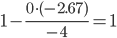
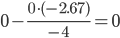
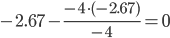
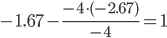
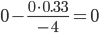
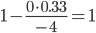
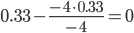
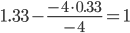
0 / -4 = 0	0 / -4 = 0	-4 / -4 = 1	-4 / -4 = 1

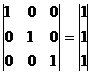
Ответ: x₁ = 1, x₂ = 1, x₃ = 1

Показатель	Метод Гаусса	Метод Жордано-Гаусса
Вид матрицы	Треугольная матрица	Единичная матрица
Время решения	0.031	0.022
Объем используемой памяти, байт	5647	3277

Реализация метода Гаусса

Метод Гаусса реализован на многих языках программирования, в частности: Pascal, C++, php, Delphi, а также имеется реализация метода Гаусса в онлайн режиме.

Использование метода Гаусса

Применение метода Гаусса в теории игр

В теории игр при отыскании максиминной оптимальной стратегии игрока составляется система уравнений, которая решается методом Гаусса.

Применение метода Гаусса при решении дифференциальных уравнений

Для поиска частного решения дифференциального уравнения сначала находят производные соответствующей степени для записанного частного решения (y=f(A,B,C,D)), которые подставляют в исходное уравнение. Далее, чтобы найти переменные A,B,C,D составляется система уравнений, которая решается методом Гаусса.

Применение метода Жордано-Гаусса в линейном программировании

В линейном программировании, в частности в симплекс-методе для преобразования симплексной таблицы на каждой итерации используется правило прямоугольника, в котором используется метод Жордано-Гаусса.

Примеры

Пример №1. Решить систему методом Гаусса:
x₁ +2x₂ - 3x₃ + x₄ = -2
x₁ +2x₂ - x₃ + 2x₄ = 1
3x₁ -x₂ + 2x₃ + x₄ = 3
3x₁ +x₂ + x₃ + 3x₄ = 2

Решение
Видео решение

Решение находим с помощью калькулятора.
Запишем систему в виде: Решение методом Гаусса

Для удобства вычислений поменяем строки местами:

Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой

Умножим 2-ую строку на (3). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой

Умножим 4-ую строку на (-1). Добавим 4-ую строку к 3-ой

Для удобства вычислений поменяем строки местами:

Умножим 1-ую строку на (0). Добавим 2-ую строку к 1-ой

Умножим 2-ую строку на (7). Умножим 3-ую строку на (2). Добавим 3-ую строку к 2-ой

Умножим 1-ую строку на (15). Умножим 2-ую строку на (2). Добавим 2-ую строку к 1-ой

Из 1-ой строки выражаем x₄

Из 2-ой строки выражаем x₃

Из 3-ой строки выражаем x₂

Из 4-ой строки выражаем x₁

Пример №3.

Решить СЛАУ методом Жордано-Гаусса. Запишем систему в виде:

5 -1 -1 3
1 2 3 6
4 3 2 9
Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.
Разрешающий элемент равен (5). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
НЭ = СЭ - (А*В)/РЭ
РЭ - разрешающий элемент (5), А и В - элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.

1 -0.2 -0.2 0.6
0 2.2 3.2 5.4
0 3.8 2.8 6.6
Разрешающий элемент равен (2.2). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.

1 0 0.0909 1.09
0 1 1.45 2.45
0 0 -2.73 -2.73
Разрешающий элемент равен (-2.73). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.

1 0 0 1
0 1 0 1
0 0 1 1
x₁ = 1.00, x₂ = 1.00, x₃ = 1.00
Перейти к решению своей задачи

Example1
Систему линейных уравнений решить методом Гаусса
Пример
Посмотрите, как быстро можно определить, является ли система совместной
Применяя метод Гаусса исключения неизвестных, решить систему линейных уравнений. Сделать проверку найденного решения: Решение
Example 4
Решить систему уравнений методом Гаусса. Рекомендуется преобразования, связанные с последовательным исключением неизвестных, применять к расширенной матрице данной системы. Сделать проверку полученного решения.
Решение:xls
Решить систему линейных уравнений тремя способами: а) методом Гаусса последовательных исключений неизвестных; б) по формуле x = A^-1b с вычислением обратной матрицы A^-1; в) по формулам Крамера.
Решение:xls
Решить методом Гаусса следующую вырожденную систему уравнений.
Скачать решение doc
Решите методом Гаусса систему линейных уравнений записанную в матричной форме:
7 8 -3 x 92
2 2 2 y = 30
-9 -10 5 z -114

Перейти к онлайн решению своего примера

Решение системы уравнений методом сложения

Решите 6x+5y=3, 3x+3y=4 систему уравнений методом сложения.
Решение.
6x+5y=3
3x+3y=4
Умножим второе уравнение на (-2).
6x+5y=3
-6x-6y=-8
============ (складываем)
-y=-5
Откуда y = 5
Находим x:
6x+5*5=3 или 6x=-22
Откуда x = -22/6 = -11/3

Пример №2. Решение СЛАУ в матричной форме означает, что исходную запись системы необходимо привести к матричной (так называемая расширенная матрица). Покажем это на примере.
Запишем систему в виде расширенной матрицы:

2	4	3
-2	5	4
3	0	1

Добавим 2-ую строку к 1-ой:

0	9	7
-2	5	4
3	0	1

Умножим 2-ую строку на (3). Умножим 3-ую строку на (2). Добавим 3-ую строку к 2-ой:

0	9	7
0	15	14
3	0	1

Умножим 1-ую строку на (15). Умножим 2-ую строку на (-9). Добавим 2-ую строку к 1-ой:

0	0	-21
0	15	14
3	0	1

-21

Теперь исходную систему можно записать как:
x₃ = -21/(-21) = 1
x₂ = [29 - (14x₃)]/15
x₁ = [4 - (x₃)]/3
Из 2-ой строки выражаем x₂:

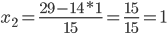
Из 3-ой строки выражаем x₁:

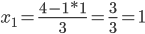
Пример №3. Решить систему методом Гаусса: x₁ +2x₂ - 3x₃ + x₄ = -2
x₁ +2x₂ - x₃ + 2x₄ = 1
3x₁ -x₂ + 2x₃ + x₄ = 3
3x₁ +x₂ + x₃ + 3x₄ = 2

Решение:
Запишем систему в виде: Решение методом Гаусса
Для удобства вычислений поменяем строки местами:

Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой

Умножим 2-ую строку на (3). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой

Умножим 4-ую строку на (-1). Добавим 4-ую строку к 3-ой

Для удобства вычислений поменяем строки местами:

Умножим 1-ую строку на (0). Добавим 2-ую строку к 1-ой

Умножим 2-ую строку на (7). Умножим 3-ую строку на (2). Добавим 3-ую строку к 2-ой

Умножим 1-ую строку на (15). Умножим 2-ую строку на (2). Добавим 2-ую строку к 1-ой

Из 1-ой строки выражаем x₄

Из 2-ой строки выражаем x₃

Из 3-ой строки выражаем x₂

Из 4-ой строки выражаем x₁

1	-0.2	-0.2	0.6
0	2.2	3.2	5.4
0	3.8	2.8	6.6

1	0	0.0909	1.09
0	1	1.45	2.45
0	0	-2.73	-2.73