Решение линейных дифференциальных уравнений
Назначение сервиса. Данный онлайн-калькулятор служит для решения линейного дифференциального уравнения с постоянными коэффициентами видаay(n)+by+c=R(x). Например, y''-2y=0, 2y''+y'-2y=x2. Решение оформляется в формате Word. Для решения уравнений вида y'+x*y=x2 используйте этот калькулятор.
y''-2y=0 максимальная степень равна двум, поэтому n=2, для y'''-2y''-y=0 степень равна трем (n=3).
Пример 1. Общее решение дифференциального уравнения с правой частью:
1. Для уравнения y''' - 4y'' + 5y' – 2y = 2x+3 корнями характеристического уравнения r3 – 4r2 + 5r – 2 = 0 являются r=2 кратности 1 и r=1 кратности 2. Следовательно α+β i=0 и не является корнем характеристического уравнения. Поэтому k=0 и частное решение ищем в виде y = cx + d. Так как y’ = 0, y’’ = 0, y’’’ = 0, то, подставляя в уравнение, получаем 5c - 2cx - 2d = 2x + 3. Приравнивая коэффициенты при одинаковых степенях x, получаем -2c = 2. -5c – 2d = 3. Следовательно, c=-1, d= -4 и y = -x-4 - частное, а y = -x-4+C1ex + C2e2x - общее решения уравнения.
2. Для уравнения y''' - 4y'' + 5y' – 2y = (2x+3)e2x число α+β i=2 является корнем характеристического уравнения кратности 1. Поэтому частное решение ищем в виде y = x(cx + d)e2x.
3. Для уравнения y’’ + y = cos(x) корнями характеристического полинома r2+1 являются числа r = ±i кратности 1. Поэтому частное решение ищем в виде y=x(a1cosx + a2 sinx). Тогда
y’ = (a1 + a2x)cosx + (a2 – a1x)sinx,
y’’ = (2a2 – a1x)cosx + (-2a1-a2x)sinx
Подставляя в исходное уравнение и приводя подобные, получаем 2a2 cosx – 2a1sinx = cosx, откуда a1 = 0;a2=0,5.
4. Найти общее решение уравнения:
Находим решение однородного уравнения y'' - 3y' + 2y = 0.
Характеристическое уравнение:
r2-3r+2=0 имеет корни r1= 1, r2= 2.
Общее решение уравнения без правой части равно:
yОбщ = C1ex + C2e2x
Правая часть уравнения имеет вид R(x) = P(x)eαx, причем P(x) = x2 + 3x и число α = 0 не является корнем характеристического уравнения. Ищем решение вида:
2Ax2 + (2B - 6A)x + 2C - 3B + 2A = x2 + 3x
Приравнивая коэффициенты при одинаковых степенях х, получаем систему:
2A = 1; 2B - 6A = 3; 2C - 3B + 2A = 0,
из которых находим: A = 1/2, B = 3, C = 4, так что
y* = x2/2 + 3x + 4
Общее решение дифференциального уравнения есть:
5. Найти общее решение уравнения: y'' - 3y' = x2 + 3x
Характеристическое уравнение: r2 - 3r = 0 имеет корни r1= 3, r2= 0.
Общее решение уравнения без правой части равно:
Приравнивая коэффициенты при одинаковых степенях х, получаем систему:
-9A = 1, -6B + 6A = 3, -3C + 2B = 0,
из которых находим: A = -1/9, B = -11/18, C = -11/27, так что
y* = x2/9 - 11x/18 -11/27
Общее решение дифференциального уравнения есть:
Пример 2. Решить дифференциальное уравнение 8y'' +2y' - 3y = 0.
Решение. Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
8r2 +2r - 3 = 0
D = 22 - 4·8·(-3) = 100
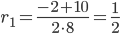 ,
, 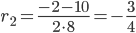
Корни характеристического уравнения: r1 = 1/2, r2 = -3/4
Следовательно, фундаментальную систему решений составляют функции: y1 = e1/2x, y2 = e-3/4x
Общее решение однородного уравнения имеет вид: 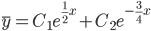
Найдем частное решение при условии: y(0) = -6, y'(0) = 7
Поскольку y(0) = c1+c2, то получаем первое уравнение:
c1+c2 = -6
Находим первую производную:
y' = 1/2•c1•e1/2•x-3/4•c2•e-3/4•x
Поскольку y'(0) = 1/2•c1-3/4•c2, то получаем второе уравнение:
1/2•c1-3/4•c2 = 7
В итоге получаем систему из двух уравнений:
c1+c2 = -6
1/2•c1-3/4•c2 = 7
которую решаем или методом матриц или методом исключения переменных.
c1 = 2, c2 = -8
Тогда частное решение при заданных начальных условиях можно записать в виде: 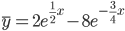
см. также Дифференциальные уравнения. Пример решения.
Если правая часть уравнения отлична от нуля, то решение ищется по формуле: R(x)=eαx(P1cos(βx)+P2sin(βx))
| R(x) | Форма записи решения |
| 10•x•e2x | (Ax + B)e2x |
| x•e-x•cos(3x) | e-x((Ax+B)cos(3x)+(Cx+D)sin(3x)) |
| (x3-x2+3)cos(x)-x•sin(x) | (Ax3+Bx2+Cx+D)cos(x)+(Ex3+Fx2+Gx+H)sin(x) |
| cos(x) | Acos(x) + Bsinx(x) |
| x•sin(x) | (Ax + B)cos(x) + (Cx + D)sinx(x) |
| x3-x2+3 | Ax3+Bx2+Cx+D |

