Уравнения, допускающие понижение порядка
Мы умеем решать уравнения первого порядка. Поэтому возникает естественное желание свести уравнение порядка выше первого к уравнению более низкого порядка. В некоторых случаях это удаётся сделать. Рассмотрим их.1. Уравнения вида y(n)=f(x) решаются последовательным интегрированием n раз
, 
,… .
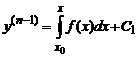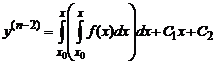Пример №1. Решить уравнение xy''=1. Можем записать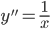 
, следовательно, y'=ln|x| + C1и, интегрируя ещё раз, окончательно получаем y=∫ln|x| + C1x + C2
2. В уравнениях вида F(x,y(k),y(k+1),..,y(n))=0 (то есть не содержащих в явном виде неизвестной функции и некоторых её производных) порядок понижается с помощью замены переменной y(k) = z(x). Тогда y(k+1)=z'(x),…,y(n) = z(n-k)(x) и мы получаем уравнение F(x,z,z',..,z(n-k)) порядка n-k. Его решением является функция z = φ(x,C1,C2,…,Cn) или, вспоминая, что такое z, получаем уравнение y(n-k) = φ(x,C1,C2,…,Cn-k) рассмотренного в случае 1 типа.
Пример №2. Решить уравнение x2y'' = (y')2. Делаем замену y'=z(x). Тогда y''=z'(x). Подставляя в исходное уравнение, получаем x2z'=z2. Разделяя переменные, получаем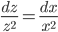 
. Интегрируя, имеем 
, или, что тоже самое, 
. Последнее соотношение записывается в виде 
, откуда 
. Интегрируя, окончательно получаем 
Пример №3. Решить уравнение x3y'' +x2y'=1 .Делаем замену переменных: y'=z; y''=z'
x3z'+x2z=1. Делаем замену переменных: z=u/x; z'=(u'x-u)/x2
x3(u'x-u)/x2+x2u/x=1 или u'x2-xu+xu=1 или u'x^2=1. Откуда: u'=1/x2 или du/dx=1/x2 или u = int(dx/x2) = -1/x+c1
Поскольку z=u/x, то z = -1/x2+c1/x. Поскольку y'=z, то dy/dx=-1/x2+c1/x
y = int(c1dx/x-dx/x2) =c1ln(x) + 1/x + c2. Ответ: y = c1ln(x) + 1/x + c2
3. Следующим уравнением, допускающим понижение порядка, является уравнение вида F(y,y',y'',…,y(n))=0, не содержащее в явном виде независимой переменной. Порядок уравнения понижается с помощью замены переменной y'=p(y), где p - новая искомая функция, зависящая от y. Тогда
= 
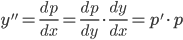
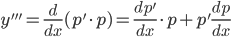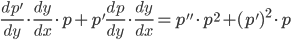и так далее. По индукции имеем y(n)=φ(p,p',..,p(n-1)). Подставляя в исходное уравнение, понижаем его порядок на единицу.
Пример №4. Решить уравнение (y')2+2yy''=0. Делаем стандартную замену y'=p(y), тогда y″=p′·p. Подставляя в уравнение, получаем 
Разделяя переменные, при p≠0, имеем 
Интегрируя, получаем 
или, что то же самое, 
. Тогда
или 
. Интегрируя последнее равенство, окончательно получаем 
При разделении переменных мы могли потерять решение y=C, которое получается при p=0, или, что то же самое, при y'=0, но оно содержится в полученном выше.
4. Иногда удаётся подметить особенность, позволяющую понизить порядок уравнения отличными от рассмотренных выше способами. Покажем это на примерах.
Замечания.
1. Если обе части уравнения yy'''=y′y″ разделить на yy″, то получим уравнение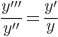 
, которое можно переписать в виде (lny″)′=(lny)′. Из последнего соотношения следует, что lny″=lny+lnC, или, что то же самое, y″=Cy. Получилось уравнение на порядок ниже и рассмотренного ранее типа.
2. Аналогично для уравнения yy″=y′(y′+1) имеем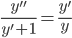 
, или (ln(y'+1))' = (lny)'. Из последнего соотношения следует, что ln(y'+1) = lny + lnC1, или y'=C1y-1. Разделяя переменные и интегрируя, получаем, ln(C1y-1) = C1x+C2
