Уравнения Бернулли
Дифференциальное уравнениеy' +a0(x)y=b(x)yn называется уравнением Бернулли.
Так как при n=0 получается линейное уравнение, а при n=1 - с разделяющимися переменными, то предположим, что n ≠ 0 и n ≠ 1. Разделим обе части (1) на yn. Тогда
Положив 
, имеем 
. Подставляя это выражение, получим 
, или, что то же самое, z' + (1-n)a0(x)z = (1-n)b(x). Это линейное уравнение.
Назначение сервиса. Онлайн калькулятор можно использовать для проверки решения дифференциальных уравнений Бернулли.
Пример 1. Найти общее решение уравнения y' + 2xy = 2xy3. Это уравнение Бернулли при n=3. Разделив обе части уравнения на y3 получаем 
Делаем замену 
Тогда 
и поэтому уравнение переписывается в виде -z' + 4xz = 4x. Решая это уравнение методом вариации произвольной постоянной, получаем 
откуда 
или, что то же самое, 
.
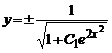Пример 2. y'+y+y2=0
y'+y = -y2
Разделим на y2
y'/y2 + 1/y = -1
Делаем замену:
z=1/yn-1, т.е. z = 1/y2-1 = 1/y
z = 1/y
z'= -y'/y2
Получаем: -z' + z = -1 или z' - z = 1
Далее надо найти z и выразить через него y = 1/z.
Пример 3. xy’+2y+x5y3ex=0
Решение.
а) Решение через уравнение Бернулли.
Представим в виде: xy’+2y=-x5y3ex. Это уравнение Бернулли при n=3. Разделив обе части уравнения на y3 получаем: xy'/y3+2/y2=-x5 ex. Делаем замену: z=1/y2. Тогда z'=-2/y3 и поэтому уравнение переписывается в виде: -xz'/2+2z=-x5ex. Это неоднородное уравнение. Рассмотрим соответствующее однородное уравнение: -xz'/2+2z=0
1. Решая его, получаем: z'=4z/x
Интегрируя, получаем: 
ln(z) = 4ln(z)
z=x4. Ищем теперь решение исходного уравнения в виде: y(x) = C(x)x4, y'(x) = C(x)'x4 + C(x)(x4)'
-x/2(4C(x) x3+C(x)' x4)+2y=-x5ex
-C(x)' x5/2 = -x5ex или C(x)' = 2ex. Интегрируя, получаем: C(x) = ∫2exdx = 2ex+C
Из условия y(x)=C(x)y, получаем: y(x) = C(x)y = x4 (C+2ex) или y = Cx4+2x4ex. Поскольку z=1/y2, то получим: 1/y2 = Cx4+2x4ex
б) решение через замену переменных
y=uv
x(u'v + uv')+2uv+x5u3v3ex=0
v(x u' + 2u) + xuv'+ x5u3v3ex = 0
a) xu'+2u = 0
или ln(u)=ln(x-2). Откуда u = x-2
b) xuv'+ x5u3v3ex = 0
x x-2v'+ x5 x-6v3ex = 0
v'/x+ v3ex/x = 0
v'+ v3ex = 0
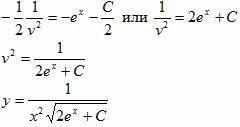или 1/y2 = Cx4+2x4ex
