Однородные дифференциальные уравнения
Если уравнение удается преобразовать к видуM(x,y)dx + N(x,y)dy = 0 является однородным тогда и только тогда, когда функции M(x,y) и
N(x,y) однородные функции одной и той же степени.
Однородное дифференциальное уравнение сводится к уравнению с разделяющимися переменными заменой y = xu, или, что тоже самое, ![]() , где u новая искомая функция. Действительно, тогда y' = u + u'x и исходное уравнение может быть переписано в виде u + u'x = f(u), или u'x = f(u)u. Из последнего при f(u)u можем записать
, где u новая искомая функция. Действительно, тогда y' = u + u'x и исходное уравнение может быть переписано в виде u + u'x = f(u), или u'x = f(u)u. Из последнего при f(u)u можем записать ![]() .
.
Пример. Решить уравнение (y2 - 2xy)dx + x2dy = 0. Это однородное уравнение, так как y2 - 2xy и x2 однородные функции второй степени. Делаем замену y = xu, dy = udx + xdu. Подставляя в уравнение, имеем
(x2u2 - 2x2u)dx + x2(udx + xdu) = 0.
Раскрывая скобки, приводя подобные и сокращая на x2, получаем уравнение с разделяющимися переменными
(u2 - u)dx + xdu = 0
Разделяя переменные, получаем ![]() или, что то же самое,
или, что то же самое, ![]() Интегрируя последнее соотношение, имеем lnu - ln(u-1) = lnx + lnC. Потенцируя (переходя от логарифмической функции к ex), можем записать
Интегрируя последнее соотношение, имеем lnu - ln(u-1) = lnx + lnC. Потенцируя (переходя от логарифмической функции к ex), можем записать ![]() или, делая обратную замену
или, делая обратную замену
![]() , получаем общий интеграл уравнения
, получаем общий интеграл уравнения ![]()
Уравнения вида![]() приводятся к однородным переносом начала координат в точку пересечения прямых a1x + b1y +c1 = 0, a2x + b2y +c2 = 0,
если определитель
приводятся к однородным переносом начала координат в точку пересечения прямых a1x + b1y +c1 = 0, a2x + b2y +c2 = 0,
если определитель ![]() отличен от нуля, и заменой a1x + b1y = z, если этот определитель равен нулю.
отличен от нуля, и заменой a1x + b1y = z, если этот определитель равен нулю.
Решить однородные уравнения онлайн можно с помощью специального сервиса Дифференциальные уравнения онлайн
.
Пример №1.
В однородном уравнении делаем замену переменных:
Тогда: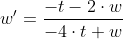
Представим в виде:
Сделаем замену переменных: w=u*t, w' = u't + u.
или
Представим в виде: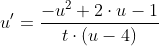
Преобразуем уравнение так, чтобы получить уравнение с разделяющимися переменными: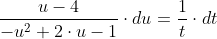
Интегрируя, получаем: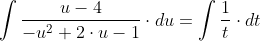
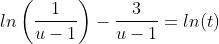
Учитывая, что w = u*t, u=w/t получаем: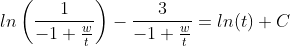
С учетом того, что:
Получаем: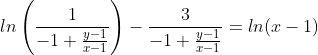
Пример №2. 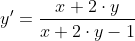
Делаем замену переменных:
Тогда: 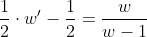
Это однородное уравнение. Представим его в виде: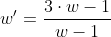
или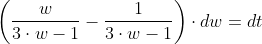
Интегрируя, получаем: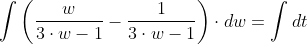
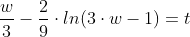
С учетом того, что:
Получаем: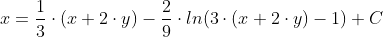
Решение было получено и оформлено с помощью сервиса:
Дифференциальные уравнения онлайн
