Уравнения в полных дифференциалах
Рассмотрим дифференциальное уравнениеM(x,y)dx+N(x,y)dy=0
Если существует функция u(x,y) такая, что
du(x,y)=M(x,y)dx+N(x,y)dy, то уравнение называется уравнением в полных дифференциалах. В этом случае его можно записать в виде du(x,y)=0.
Тогда его общий интеграл имеет вид
u(x,y)=C.
Назначение сервиса. Онлайн калькулятор можно использовать для проверки решения дифференциальных уравнений в полных дифференциалах и для поиска интегрирующего множителя.
Примеры
1. Дифференциальное уравнение xdy+ydx=0 является уравнением в полных дифференциалах, так как d(xy)= xdy+ydx. Поэтому xy=C есть общее решение этого уравнения.
2. Аналогично для уравнения 2xydx+x2dy=0 выражение x2y=C есть общее решение, так как левая часть этого уравнения является дифференциалом функции u(x,y)=x2y.
Сравнивая с определением потенциальности поля (M,N)T, получаем справедливость следующего результата.
Теорема. Уравнение (1) есть уравнение в полных дифференциалах тогда и только тогда, когда поле (M,N)T потенциально, или, что тоже самое, криволинейный интеграл 
не зависит от пути интегрирования.
Следствие. Если существуют непрерывные производные 
то уравнение (1) есть уравнение в полных дифференциалах тогда и только тогда, когда 
Следствие даёт возможность выяснить является ли уравнение уравнением в полных дифференциалах или нет. Теорема позволяет найти решение уравнения в случае положительного ответа на предыдущий вопрос.
Примеры
1. Найти общее решение уравнения 2xydx+(x2-y2)dy=0. Так как 
то данное уравнение является уравнением в полных дифференциалах. Поэтому, восстанавливая потенциал, получаем
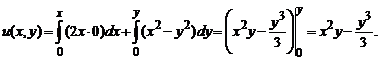Тогда общий интеграл (общее решение) имеет вид 
2. Уравнение e-ydx-(2y+xe-y)dy=0 также является уравнением в полных дифференциалах, так как
Поэтому, восстанавливая потенциал, имеем
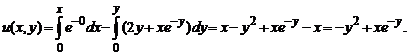
Следовательно, общий интеграл уравнения равен: -y2+xe-y=C.