Линейные дифференциальные уравнения высших порядков
Рассмотрим множество M[a,b] всех определённых на отрезке [a,b] функций. На этом множестве введём операции:1) сложения элементов f1,f2∈[a,b] по правилу:
(f1+f2)(x) = f1(x)+f2(x) для ∀x∈[a,b].
2) умножения элемента f∈M[a,b] на скаляр a∈R по закону (a·f)(x)=a·f(x) для ∀x∈[a,b].
Относительно введённых операций M[a,b] является линейным пространством, так как выполнены все аксиомы линейного пространства [1,2,12].
Рассмотрим два подмножества множества M[a,b]:
C[a,b] - множество непрерывных на [a,b] функций;
Cn[a,b]- множество n раз непрерывно дифференцируемых на отрезке [a,b] функций.
Отметим, что имеет место поэлементное включение Cn[a,b]⊂C[a,b]⊂M[a,b]. Так как введённые линейные операции не выводят за пределы множеств C[a,b] и Cn[a,b] соответственно, то они являются линейными подпространствами пространства M[a,b]. Следовательно, как самостоятельные объекты, они являются линейными пространствами. В отличие от рассмотренных в линейной алгебре пространств, введённые пространства бесконечномерные.
Определим оператор L:Cn[a,b]→C[a,b] следующим образом
,
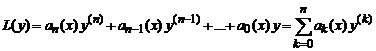
то можно записать
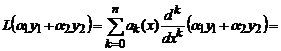
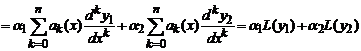
Уравнение вида L(y)=b(x), где b(x)- некоторая функция, а L(y)- введённый выше оператор, называется линейным дифференциальным уравнением n-го порядка. Иногда будем пользоваться подробными записями этого уравнения
an(x)y(n) + an-1(x)y(n-1) + … + a1(x)y' + a0(x)y = b(x), (5.23)
или
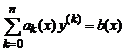. (5.23а)
Так же, как и для уравнений первого порядка, для линейных уравнений порядка n теорема существования и единственности имеет более конкретный вид.
Теорема. Пусть функции ak(x), 0≤k≤n, и b(x) определены и непрерывны на отрезке [α, β] и пусть x0 - некоторая точка этого отрезка. Тогда для любого набора начальных данных (5.20) (y(x0)=y00, y′(x0)=y10, ... , y(n-1)(x0)=yn-10) существует единственное решение уравнения (5.23), определённое на всём отрезке [α, β].
Доказательство этого результата опустим.
Отметим, что свойства решений линейных дифференциальных уравнений L(y)=b(x) и L(y)=0 подобны свойствам решений систем линейных алгебраических уравнений Ax=B и Ax=0. Приведём эти свойства.
Теорема (о наложении решений). Если y1,y2- решения уравнений L(y)=b1 и L(y)=b2 соответственно, то линейная комбинация α1y1+ α2y2 есть решение уравнения L(y) = α1b1+ α2b2.
Доказательство. В силу линейности оператора L имеем L(α1y1+ α2y2) = α1L(y1)+ α2L(y2) = α1b1+ α2b2. Теорема доказана.
Следствие. Если y1- решение уравнения L(y)=b1, y2- решение уравнения L(y)=0, то y1+y2- решение уравнения L(y)=b1.
Следствие. Любая линейная комбинация решений уравнения L(y)=0 снова есть решение этого уравнения.
Доказательство. Пусть y1,y2,..,ym есть решения уравнения L(y)=0. Тогда
.
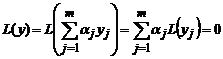Следствие доказано.
Следствие. Множество всех решений уравнения L(y)=0 образует линейное подпространство пространства Cn[a,b].
Доказательство. По предыдущему следствию линейные операции над решениями уравнения L(y)=0 не выводят за пределы множества решений этого уравнения, что и доказывает следствие.
Определение. Любой базис пространства решений линейного однородного дифференциального уравнения n-го порядка называется фундаментальной системой решений этого уравнения.
Так же как и в линейной алгебре, имеет место следующий результат.
Теорема (о виде общего решения линейного неоднородного дифференциального уравнения). Общее решение линейного неоднородного дифференциального уравнения L(y)=b есть сумма общего решения соответствующего однородного уравнения и какого либо частного решения неоднородного уравнения.
Доказательство теоремы аналогично доказательству теоремы о виде общего решения линейного однородного дифференциального уравнения и поэтому мы его опустим.
Решить линейные дифференциальные уравнения высших порядков онлайн можно с помощью специального сервиса Дифференциальные уравнения онлайн.