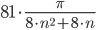Признаки сходимости ряда
Определение. Числовым рядом называется бесконечная сумма членов последовательности: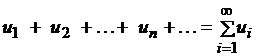 .
.
Признаки сходимости знакопостоянного числового ряда можно разделить на необходимый и достаточные.
Необходимый признак сходимости состоит в том, что:
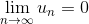 .
.
Если этот признак не выполняется, то ряд расходится.
Для степенного ряда
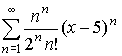 используйте этот калькулятор.
используйте этот калькулятор.
Правила ввода данных
- В качестве переменной используйте только n.
- Все математические операции выражаются через общепринятые символы (+ , - , * , / , ^ ). Например,
4n, записываем как 4^n.
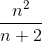 ≡ n^2/(n+2)
≡ n^2/(n+2)
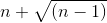 ≡ n+sqrt(n-1)
≡ n+sqrt(n-1)
Правила ввода данных
- Все математические операции выражаются через общепринятые символы ( + , - , * , / , ^ ). Например, 4n, записываем как 4^n.
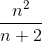 ≡ n^2/(n+2)
≡ n^2/(n+2)
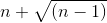 ≡ n+sqrt(n-1)
≡ n+sqrt(n-1)
Рассмотрим четыре достаточных признака сходимости числового ряда 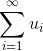 .
.
1. Признак Даламбера.
Если 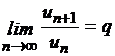 , то
, то 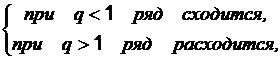
при q = 1 получаем неопределенность.
2. Радикальный признак Коши.
Если ![]() ,
, 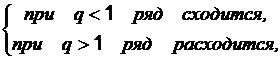
при q = 1 получаем неопределенность.
3. Интегральный признак Коши.
Если 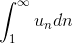 существует, то ряд сходится; если интеграл не существует (т. е. равен ±∞) – ряд расходится.
существует, то ряд сходится; если интеграл не существует (т. е. равен ±∞) – ряд расходится.
4. Признак сравнения.
Если 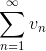 сходится и un ≤ vn, то
сходится и un ≤ vn, то 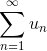 также сходится, если
также сходится, если 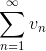 расходится и un ≥ vn, то
расходится и un ≥ vn, то 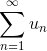 также расходится.
также расходится.
Для признака сравнения в качестве ряда 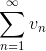 часто используется
часто используется 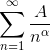 , который
, который 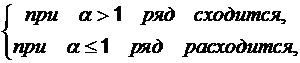 , A - произвольная постоянная величина; причем
, A - произвольная постоянная величина; причем 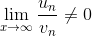 .
.
5. Предельный признак сравнения.
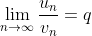
Если предел отношений исходного ряда un с расходимым рядом vn равен конечному числу, отличному от нуля, то ряд un расходится.
Если предел отношений исходного ряда un со сходимым рядом vn равен конечному числу, отличному от нуля, то ряд vn сходится.
Схема определения сходимости или расходимости ряда
Пример 1. Исследовать ряд 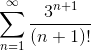 на сходимость.
на сходимость.
Решение:
Применим признак Даламбера:
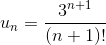 ;
; 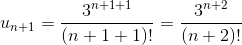
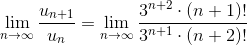 =
= 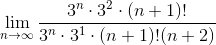 =
= 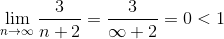 ряд сходится.
ряд сходится.
Пример 2. Исследовать ряд 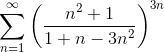 на сходимость.
на сходимость.
Решение:
Применим радикальный признак Коши:
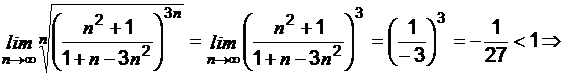 ряд сходится.
ряд сходится.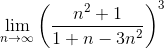 вычисляем следующим образом: так как в числителе и знаменателе дроби старшие степени переменной n равны, то выписываем коэффициенты при n2 соответственно из числителя и знаменателя.
вычисляем следующим образом: так как в числителе и знаменателе дроби старшие степени переменной n равны, то выписываем коэффициенты при n2 соответственно из числителя и знаменателя.Пример 3. Исследовать ряд 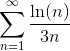 на сходимость.
на сходимость.
Решение:
Применим интегральный признак Коши:
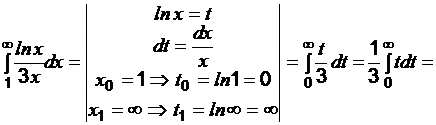
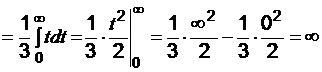 , так как интеграл не существует, то ряд расходится.
, так как интеграл не существует, то ряд расходится.Пример 4. Исследовать ряд 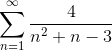 на сходимость.
на сходимость.
Решение:
Сравним ряд с 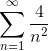 , который сходится, так как степень α переменной n: α=2 > 1. При этом
, который сходится, так как степень α переменной n: α=2 > 1. При этом 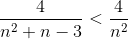 , следовательно ряд
, следовательно ряд 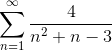 также сходится.
также сходится.
Пример 5. Исследовать ряд 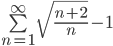 на сходимость.
на сходимость.
Решениие.
Исходное выражение преобразуем к виду:
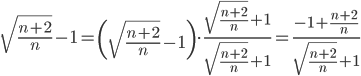
Тогда исходный ряд можно представить в виде:
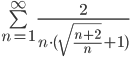
Коэффициент общего члена не влияет на сходимость или расходимость ряда, поэтому выносим его за пределы суммы:
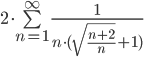
Применим сравнительный признак. Рассмотрим ряд: 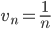 ,
, 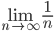 .
.
Поскольку un≤vn, то если ряд vn будет сходиться, то будет сходиться и исходный un.
По определению этот ряд расходится, здесь α≤1.
Проведя анализ ряда 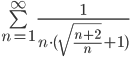 можно сделать вывод, что признак сравнения здесь не применим (по условию ряд должен был сходиться, а он расходится). Поэтому продолжаем исследования далее. Используем предельный признак сравнения.
можно сделать вывод, что признак сравнения здесь не применим (по условию ряд должен был сходиться, а он расходится). Поэтому продолжаем исследования далее. Используем предельный признак сравнения.
Сравним исследуемый ряд с расходящимся рядом: 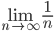
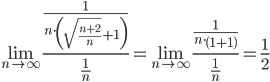
здесь 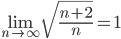
Получено конечное число, отличное от нуля, значит, исследуемый ряд расходится.
Следовательно, ряд 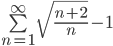 расходится.
расходится.
Преобразование и упрощение функции
- Логарифмические функции:
log(n)-log(n+1)=log(n/(n+1)) - Дополнение до квадрата:
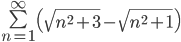
Исходное выражение преобразуем к виду: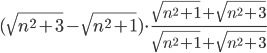 =
=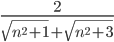
- Тригонометрическая заменна.
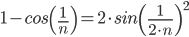
Пример,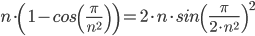
- Упрощение и сокращение
Пример,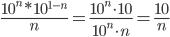
Пример,
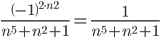
Замена на замечательные эквивалентности
- Замечательные эквивалентности в пределах
- Второй замечательный предел:
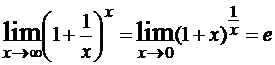
Ограниченность функции при n → ∞
cos(π n) = (-1)nsin(π n) ≈ 0cos(n) ≈ [-1;1]sin(n) ≈ [-1;1]cos2(n) ≈ [0;1]sin2(n) ≈ [0;1]
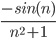 :
:
Последовательность sin(n) ограничена [-1,1]
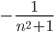 ≤
≤ 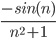 ≤
≤ 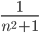
Пример,
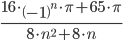 :
:
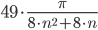 ≤
≤ 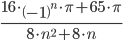 ≤
≤