Исследование степенного ряда на сходимость
Дан степенной ряд 
. Написать первые три члена ряда, найти интервал сходимости ряда и исследовать его сходимость на концах интервала.
Решение. 
- общий член ряда. Подставив в эту формулу n значения 1, 2, 3, …, можно найти любой член ряда:
,
,
.
Степенной ряд в общем виде записывается следующим образом: 
, где an – формула числовых коэффициентов. Для данного ряда 
.
Областью сходимости степенного ряда является интервал (-R;R), где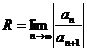 
- радиус сходимости. Вычислим его:
.
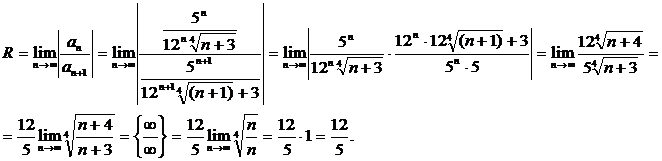
Теперь проверим сходимость ряда на концах этого интервала.
Пусть
получаем ряд 
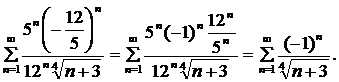
Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница:
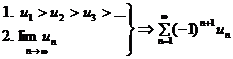сходится.
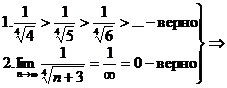ряд сходится, значит, 
- точка сходимости.
При
исходный ряд принимает вид: 
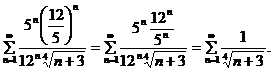- числовой знакоположительный ряд. Исследуем его сходимость при помощи интегрального признака сходимости Коши. Рассмотрим несобственный интеграл:
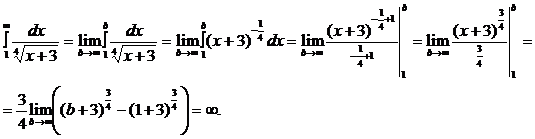
Так как несобственный интеграл расходится, то расходится и исследуемый ряд. Значит,
- точка расходимости.
Таким образом, данный степенной ряд является сходящимся при
.