Приведение кривой второго порядка к каноническому виду
Уравнение второго порядка вида
определяет на плоскости кривую. Группа членов
называется квадратичной формой, 
– линейной формой. Если в квадратичной форме содержатся только квадраты переменных, то такой ее вид называется каноническим, а векторы ортонормированного базиса, в котором квадратичная форма имеет канонический вид, называются главными осями квадратичной формы.
Матрица
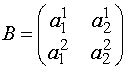называется матрицей квадратичной формы. Здесь a12=a21. Чтобы матрицу B привести к диагональному виду, необходимо за базис взять собственные векторы этой матрицы, тогда 
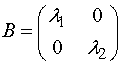, где λ1 и λ2 – собственные числа матрицы B.
В базисе из собственных векторов матрицы B квадратичная форма будет иметь канонический вид:
λ1x21+λ2y21.
Эта операция соответствует повороту осей координат. Затем производится сдвиг начала координат, избавляясь тем самым от линейной формы.
Канонический вид кривой второго порядка:
λ1x22+λ2y22=a, причем:
а) если λ1>0; λ2>0 – эллипс, в частности, при λ1=λ2 это окружность;
б) если λ1>0, λ2<0 (λ1<0, λ2>0) имеем гиперболу;
в) если λ1=0 либо λ2=0, то кривая является параболой и после поворота осей координат имеет вид
λ1x21=ax1+by1+c (здесь λ2=0). Дополняя до полного квадрата, будем иметь: λ1x22=b1y2.
Пример. Дано уравнение кривой 3x2+10xy+3y2-2x-14y-13=0 в системе координат (0,i,j), где i=(1,0) и j=(0,1).
1. Определить тип кривой.
2. Привести уравнение к каноническому виду и построить кривую в исходной системе координат.
3. Найти соответствующие преобразования координат.
Решение. Приводим квадратичную форму B=3x2+10xy+3y2 к главным осям, то есть к каноническому виду. Матрица этой квадратичной формы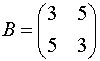 
. Находим собственные числа и собственные векторы этой матрицы:
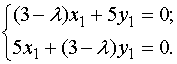
Характеристическое уравнение:
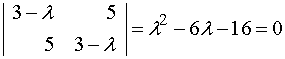; λ1=-2, λ2=8. Вид квадратичной формы: 
.
Исходное уравнение определяет гиперболу.
Заметим, что вид квадратичной формы неоднозначен. Можно записать 8x12-2y12, однако тип кривой остался тот же – гипербола.
Находим главные оси квадратичной формы, то есть собственные векторы матрицы B.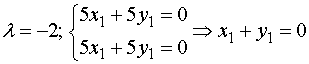 
.
Собственный вектор, отвечающий числу λ=-2 при x1=1: x1=(1,-1).
В качестве единичного собственного вектора принимаем вектор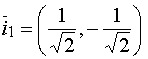 
, где 
– длина вектора x1.
Координаты второго собственного вектора, соответствующего второму собственному числу λ=8, находим из системы
.
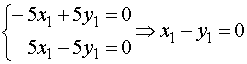x2=(1,1);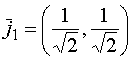 
.
Итак, имеем новый ортонормированный базис (i1,j1).
По формулам (5) пункта 4.3.3. переходим к новому базису:
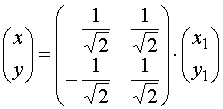или
; 
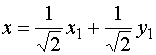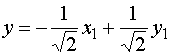. (*)Вносим выражения x и y в исходное уравнение и, после преобразований, получаем:
.
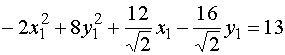Выделяем полные квадраты:
.
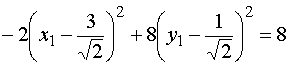Проводим параллельный перенос осей координат в новое начало:
, 
.
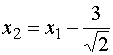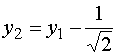Если внести эти соотношения в (*) и разрешить эти равенства относительно x2 и y2, то получим:
, 
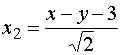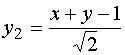. В системе координат (0*, i1, j1) данное уравнение имеет вид: 
.
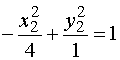Для построения кривой строим в старой системе координат новую: ось x2=0 задается в старой системе координат уравнением x-y-3=0, а ось y2=0 уравнением x+y-1=0. Начало новой системы координат 0*(2,-1) является точкой пересечения этих прямых.
Для упрощения восприятия разобьем процесс построения графика на 2 этапа:
1. Переход к системе координат с осями x2=0, y2=0, заданными в старой системе координат уравнениями x-y-3=0 и x+y-1=0 соответственно.
2. Построение в полученной системе координат графика функции.
Окончательный вариант графика выглядит следующим образом (см. как построить график):
Задание. Привести к каноническому виду уравнение линии 17x2 + 12xy + 8y2 - 20 = 0.
Решение.Пример 2
Задание. Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм и определить её вид. Уравнение кривой второго порядка путем выделения полного квадрата привести к каноническому виду. Решение
Задание. Привести уравнение к каноническому виду: 16x2 - 9y2 -64x - 8y +199 = 0.
Решение.Скачать решение
Задание. Установить, что каждое из следующих уравнений определяет гиперболу, и найти координаты ее центра С, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис. Изобразить гиперболу на чертеже, указав фокусы, асимптоты и директрисы.
Решение:Скачать решение
Задание. Установить, что каждое из следующих уравнений определяет эллипс, и найти координаты его центра С, полуоси, эксцентриситет, уравнения директрис. Изобразить эллипс на чертеже, указав оси симметрии, фокусы и директрисы.
Решение:Скачать решение
