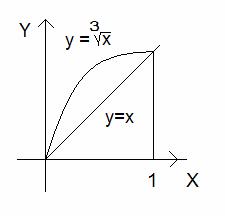Площадь фигуры, ограниченной линиями
Строить графики можно с помощью этого сервиса.Пример №1. Вычислить площадь фигуры, ограниченной линиями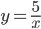 
и x+y=6.
Решение. Построим в системе координат xOy эти линии. Найдем точки пересечения этих линий
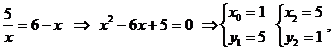
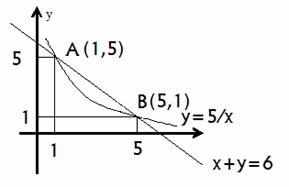
Обозначим эти точки через A и В. Итак, А(1; 5), В(5; 1). Искомая площадь S равна разности площадей фигур, ограниченных линиями x=1, x=5, y=0,y=6-x (обозначим эту площадь через S1) и линиями x=1, x=5, y=0, 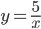(эту площадь обозначим через S2). Таким образом
S = S1 – S2 =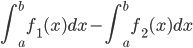 
Площадь S2 может быть вычислена с применением определенного интеграла
ед2.
Площадь S1 можно вычислить как сумму площадей прямоугольного треугольника и прямоугольника, но удобнее все-таки вычислить S1 как интеграл
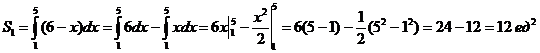
Теперь можно вычислить и искомую площадь
S = S1 – S2 = 12 – 5 ln5
Ответ: S =12 – 5 ln5 ед2.
см. также Объем фигуры, образованной в результате вращения вокруг оси: 
