Объем фигуры, образованной в результате вращения вокруг оси
Объем фигуры, образованной в результате вращения вокруг оси Ox криволинейной трапеции, ограниченной непрерывной кривой y = f(x) (a ≤ x ≤ b), Осью Ox и прямыми x= a и x = b, вычисляется по формуле: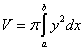
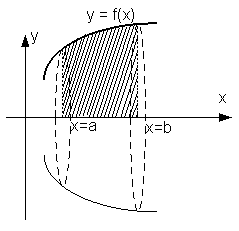
Аналогично, объем фигуры, образованной в результате вращения вокруг оси Oy криволинейной трапеции, ограниченной непрерывной кривой y = φ(x) (c ≤ x ≤ d), Осью Ox и прямыми y= c и y = d, находится по формуле:
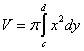
Пример №1. Вычислить объемы фигур, образованных вращением площадей, ограниченных указанными линиями.
y2 = 4x; y = 0; x = 4.

Пределы интегрирования a = 0, b = 4.
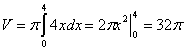
Пример №2. y2 = 4x; y = x

Выполним построение фигуры. Решим систему:
y2 = 4x
y = x
найдем точки пересечения параболы и прямой: O(0;0), A(4;4).
Следовательно, пределы интегрирования a = 0; b = 4. Искомый объем представляет собой разность объема V1 параболоида, образованного вращением кривой y2 = 4x , и о объема V2 конуса, образованного вращением прямой y = x:
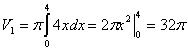
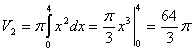
V = V1 – V2 = 32π – 64/3 π = 32/3 π
см. также как вычислить интеграл онлайн
Пример №3. Вычислить объем тела, полученного вращением вокруг оси Оx фигуры, ограниченной прямой y=x и параболой ![]() .
.
Найдем точки пересечения линий. Для этого решим уравнение ![]() . Получим x1=0, x2=1.
. Получим x1=0, x2=1.
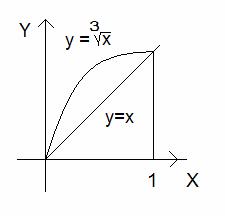
Рис. 2. Объем тела вращения.
Объем тела может быть вычислен по формуле ![]() , где
, где
![]() , f2(x)=x.
, f2(x)=x.
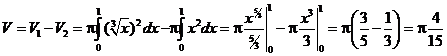
см. также Площадь фигуры, ограниченной линиями: