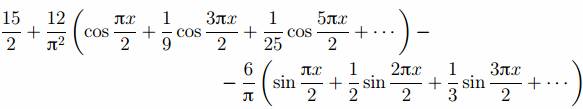Ряд Фурье
Рядом Фурье функции f(x) на интервале (-π ; π) называется тригонометрический ряд вида: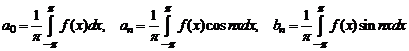
Рядом Фурье функции f(x) на интервале (-l;l) называется тригонометрический ряд вида:
![]() , где
, где
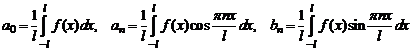
Назначение. Онлайн калькулятор предназначен для разложение функции f(x) в Ряд Фурье.
Ряд Фурье кусочно-непрерывной, кусочно-монотонной и ограниченной на интервале (-l;l) функции сходится на всей числовой оси.
Сумма ряда Фурье S(x):
- является периодической функцией с периодом 2l. Функция u(x) называется периодической с периодом T (или T-периодической), если для всех x области R, u(x+T)=u(x).
- на интервале (-l;l) совпадает с функцией f(x), за исключением точек разрыва
- в точках разрыва (первого рода, т.к. функция ограничена) функции f(x) и на концах интервала принимает средние значения:
Говорят, что функция раскладывается в ряд Фурье на интервале (-l;l):
Если f(x) – четная функция, то в ее разложении участвуют только четные функции, то есть bn=0.
Если f(x) – нечетная функция, то в ее разложении участвуют только нечетные функции, то есть аn=0
Рядом Фурье функции f(x) на интервале (0;l) по косинусам кратных дуг называется ряд:
![]() , где
, где
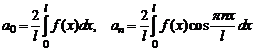 .
.
Рядом Фурье функции f(x) на интервале (0;l) по синусам кратных дуг называется ряд:
![]() , где
, где 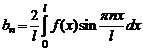 .
.
Сумма ряда Фурье по косинусам кратных дуг является четной периодической функцией с периодом 2l, совпадающей с f(x) на интервале (0;l) в точках непрерывности.
Сумма ряда Фурье по синусам кратных дуг является нечетной периодической функцией с периодом 2l, совпадающей с f(x) на интервале (0;l) в точках непрерывности.
Ряд Фурье для данной функции на данном интервале обладает свойством единственности, то есть если разложение получено каким-либо иным способом, чем использование формул, например, при помощи подбора коэффициентов, то эти коэффициенты совпадают с вычисленными по формулам.
Пример №1. Разложить функцию f(x)=1:
а) в полный ряд Фурье на интервале (-π ;π);
б) в ряд по синусам кратных дуг на интервале (0;π); построить график полученного ряда Фурье
Решение:
а) Разложение в ряд Фурье на интервале(-π;π) имеет вид:
![]() ,
,
причем все коэффициенты bn=0, т.к. данная функция – четная; таким образом,
Очевидно, равенство будет выполнено, если принять
а0=2, а1=а2=а3=…=0
В силу свойства единственности это и есть искомые коэффициенты. Таким образом, искомое разложение: ![]() или просто 1=1.
или просто 1=1.
В таком случае, когда ряд тождественно совпадает со своей функцией, график ряда Фурье совпадает с графиком функции на всей числовой прямой.
б) Разложение на интервале (0;π) по синусам кратных дуг имеет вид: ![]()
Подобрать коэффициенты так, чтобы равенство тождественно выполнялось, очевидно, невозможно. Воспользуемся формулой для вычисления коэффициентов:
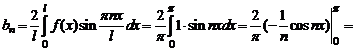
![]()
Таким образом, для четных n (n=2k) имеем bn=0, для нечетных (n=2k-1) - ![]()
Окончательно, ![]() .
.
Построим график полученного ряда Фурье, воспользовавшись его свойствами (см. выше).
Прежде всего, строим график данной функции на заданном интервале. Далее, воспользовавшись нечетностью суммы ряда, продолжаем график симметрично началу координат:

Продолжаем периодическим образом на всей числовой оси:
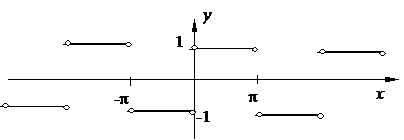
И наконец, в точках разрыва заполняем средние (между правым и левым пределом) значения:
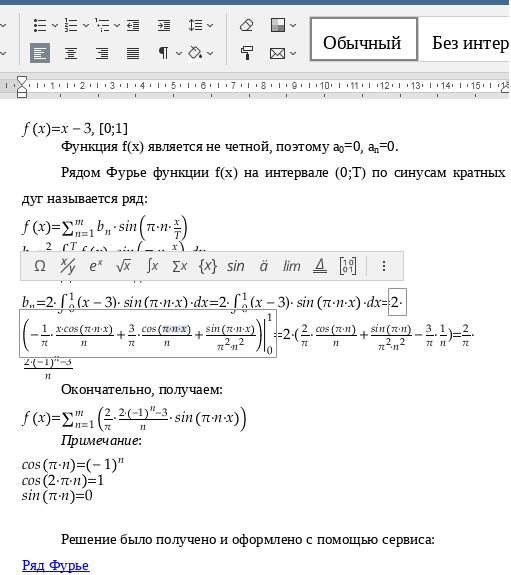
Пример №2. Разложить функцию ![]() на интервале (0;6) по синусам кратных дуг.
на интервале (0;6) по синусам кратных дуг.
Решение: Искомое разложение имеет вид:
![]()
Поскольку и левая, и правая части равенства содержат только функции sin от различных аргументов, следует проверить, совпадают ли при каких-либо значениях n (натуральных!) аргументы синусов в левой и правой частях равенства:
![]() или
или ![]() , откуда n=18. Значит, такое слагаемое содержится в правой части и коэффициент при нем должен совпадать с коэффициентом в левой части: b18=1;
, откуда n=18. Значит, такое слагаемое содержится в правой части и коэффициент при нем должен совпадать с коэффициентом в левой части: b18=1;
![]() или
или ![]() , откуда n=4. Значит, b4=-5.
, откуда n=4. Значит, b4=-5.
Таким образом, при помощи подбора коэффициентов удалось получить искомое разложение:
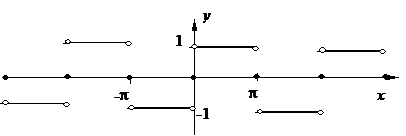
Пример №3. Разложить в ряд Фурье функцию
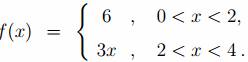
Решение. Сначала вычисляем T = 4 и ω =2π/4= π/2. Теперь находим
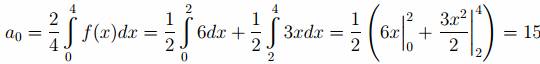
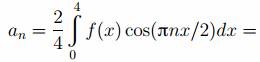
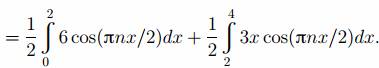
Первый интеграл находим
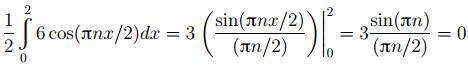
Второй интеграл берём по частям, выбирая u=3x, dv=cos(πnx/2), тогда du=3dx, v=sin(πnx/2)/(πn/2). Получаем
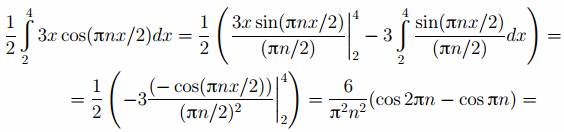
Итак, для n = 1, 3, 5, . . . an= 2/(π2n2) , а для n = 2, 4, 6, . . . an= 0.
Аналогично находим
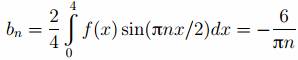
В итоге получаем разложение