Оригинал и его изображение
Изображением функции f(t) или ее преобразованием Лапласа называется функция F(p) комплексного переменного p, определяемая соотношением
. Обозначают F(p) → f(t). Правило получения по заданному оригиналу f(t) изображения F(p) называется преобразованием Лапласа.
Назначение. Данный сервис предназначен для нахождения онлайн оригинала f(t) по изображению F(p). Результаты вычисления оформляются в формате Word (см. пример).
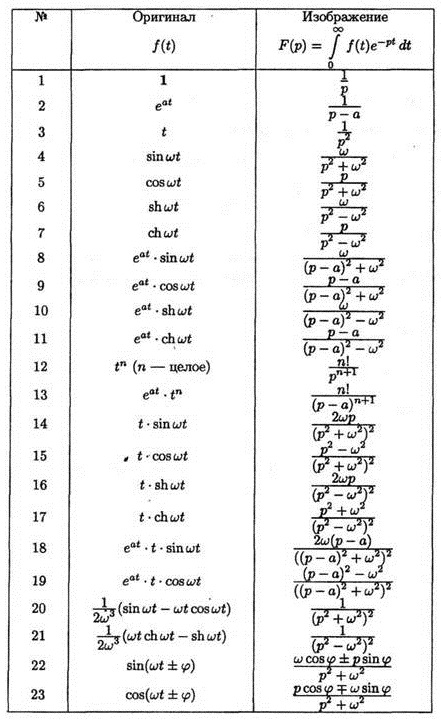
Таблица оригиналов и изображений Лапласа
| Изображение | Оригинал |
 | t |
 | 1 |
 | eat |
| sin(ωt) |
| cos(ωt) |
| e-atsin(ωt) |
| e-atcos(ωt) |
| sh(ωt) |
| ch(ωt) |
Для преобразования изображения F(p) можно использовать процедуру деления многочленов столбиком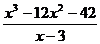 
и разложение дроби на сумму простейших дробей 
и разложение дроби на сумму простейших дробей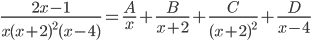 
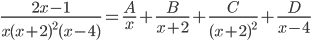
Начальной функцией или оригиналом называют функцию f(t) действительной переменной t, удовлетворяющей следующим условиям:
- f(t)=0 при t<0;
- если M>0 и s – некоторые вещественные числа, то |f(t)|≤Mest при t≥0.
- f(t) - кусочно-непрерывная и интегрируемая на любом конечном отрезке изменения t.
Теоремы запаздывания и смещения
Теорема запаздывания: L[f(t-τ)] = e-pτL[f(t)].Пример. e-2p p2+1 = η(t-2)sin(t-2)
Теорема смещения: L[ep0tf(t)] = F(p-p0).
Пример.
p+4
(p+4)2+9
= e-4tcos(3t)
