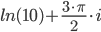Алгебраическая форма записи комплексного числа
Алгебраическая форма записи комплексного числа выглядит так:z=x+i*y, где x - действительная часть комплексного числа, y - мнимая часть.
Назначение. Онлайн калькулятор предназначен для представления комплексного числа в алгебраической форме. Результаты вычисления оформляются в формате Word.
Пример №1. Дано комплексное число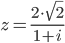 
. Требуется: 1) записать число z в алгебраической и тригонометрической формах; 2) найти все корни уравнения w3+z=0.
Решение. Предварительно с помощью данного калькулятора представим число в алгебраическая форме. Затем преобразуем число в тригонометрическую форму с помощью данного сервиса. После преобразований получим:
Алгебраическая форма записи:
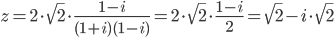
Находим тригонометрическую форму комплексного числа.
, 
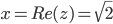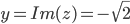
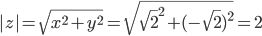
Поскольку x > 0, y < 0, то arg(z) находим как:
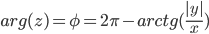
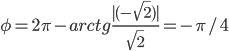
Таким образом, тригонометрическая форма комплексного числа: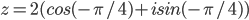
2) найти все корни уравнения w3+z=0.
Получаем уравнение w3 + z = 0 или w = (-z)1/3 = (-sqrt(2) + i*sqrt(2))1/3.
Далее решаем с помощью этого сервиса. Находим тригонометрическую форму комплексного числа z = -sqrt(2)+I*sqrt(2)
, 
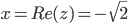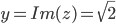
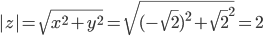
Поскольку x < 0, y ≥ 0, то arg(z) находим как: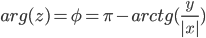
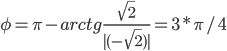
Таким образом, тригонометрическая форма комплексного числа z = -sqrt(2)+I*sqrt(2)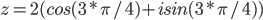
Извлекаем
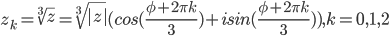
k = 0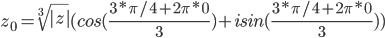
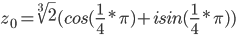
или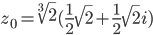
k = 1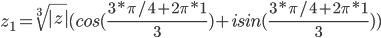
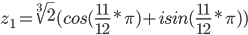
или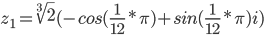
k = 2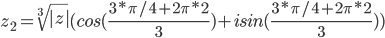
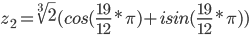
или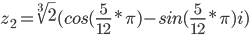
Пример №2. Дано комплексное число 
. Требуется: 1) записать число a в алгебраической и тригонометрической формах; 2) найти все корни уравнения z3 + a = 0.
Перейти к онлайн решению своей задачи
Пример №3. Число 
записать в алгебраической форме.
Решение. так как i82 = i4*20+2 = -1, i37 = i4*9+1 = i, i44 = i4*11=1, i51=i4*12+3 = -i, то
, поэтому
Пример №4. Записать число в алгебраической форме 
Решение.
Модуль числа |z|=3, аргумент argz = 5/3π
, x > 0 , y < 0
, откуда 
Имеем
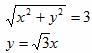
Подставим y в первое уравнение
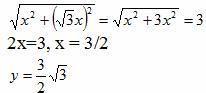
Поскольку x > 0 , y < 0, то
Пример №5. Записать число в алгебраической форме 
Решение.
Модуль числа |z|= 
, аргумент argz = 5/4π
, x < 0 , y < 0
, откуда 
Имеем
y=x
Подставим y в первое уравнение
x=1, y = 1
Поскольку x < 0 , y < 0, то z=-1-i
Пример №6. Как перевести комплексное число из показательной (экспоненциальной) формы в алгебраическую.
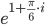
Решение. Преобразуем к виду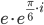 
Комплексное число представлено в экспоненциальной форме:
Аргумент числа: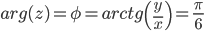 
Откуда: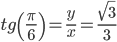 
Модуль числа: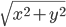 
=
Выразим y: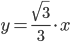
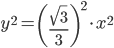
И подставим в выражение для модуля: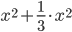
=
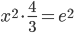
Получим: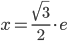 
, 
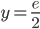
И тогда число в алгебраической форме: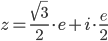 
Пример №7. Как перевести комплексное число из логарифмической формы в алгебраическую.
Решение. Представим в показательной форме:
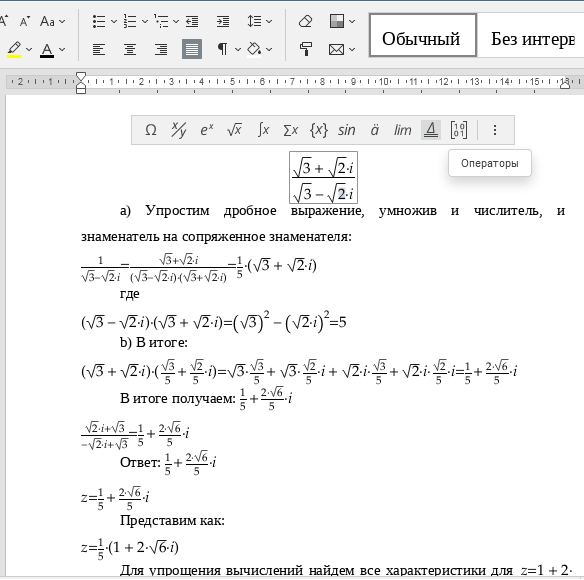
Для упрощения вычислений найдем все характеристики для
Действительная часть числа:
Мнимая часть числа:
Модуль комплексного числа:
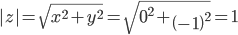
С учетом 10 получаем:
Поскольку x = 0, y < 0, то arg(z) находим как:
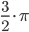
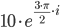
Обратно логарифмируем:
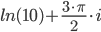
Ответ:
