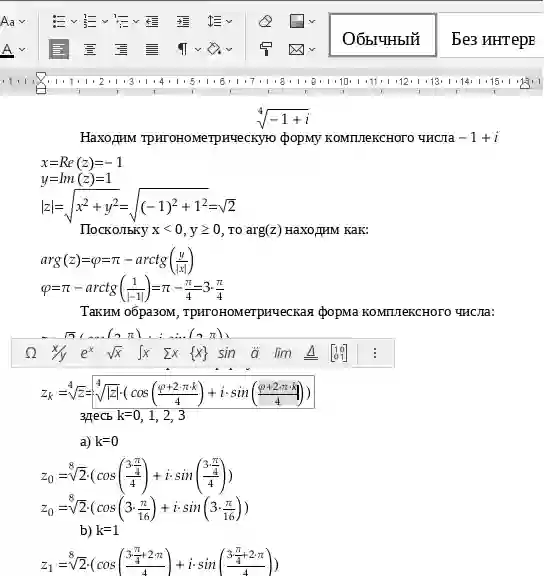
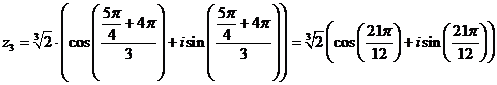Инструкция. Для получения онлайн решения необходимо отдельно ввести подкоренное выражение и степень корня.
Например, для 
необходимо ввести 1+i и 3. Корень числа вводится как sqrt, например sqrt(3).
Извлечение корня из комплексных чисел
Чтобы извлечь корень n из комплексного числа необходимо:- Найти модуль комплексного числа |z|.
- Найти аргумент комплексного числа φ.
см. также Как решать уравнения с комплексными числами, Алгебраическая форма записи комплексного числа.
Пример №1. Найдите .
Решение:
Находим тригонометрическую форму комплексного числа z = 1 + i: x = Re(z) = 1, y = Im(z) = 1 > 0,
,
.
Таким образом,
– тригонометрическая форма комплексного числа z = 1 + i.
Извлекаем
(k = 0, 1, 2). Итак,
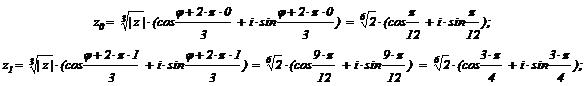
Пример №2. Найдем корень из комплексного числа. 
. Для этого перейдем в тригонометрическую форму x=-1, y=-1.
, 
.
Такой тангенс у двух углов 
и 
.
Так как х и у отрицательны, то угол находится в третьей четверти 
. n=3, m=0,1,2.
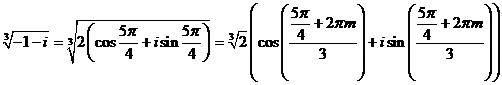
Подставим m=0
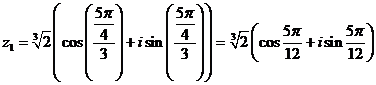
Подставим m=1
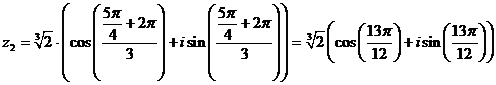
Подставим m=2
