Решение комплексных уравнений
Дано:z3+1–i=0. Представим в виде: z3=i-1, откуда выразив z, получим: Далее решаем онлайн.
Находим тригонометрическую форму комплексного числа
x = Re(z) = -1
y = Im(z) = 1
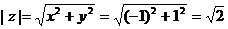
Поскольку x < 0, y ≥ 0, то arg(z) находим как:
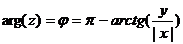
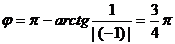
Таким образом, тригонометрическая форма комплексного числа z = I-1
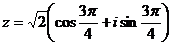
z=I-1
x = Re(z) = -1
y = Im(z) = 1
Поскольку x < 0, y ≥ 0, то arg(z) находим как:
Таким образом, тригонометрическая форма комплексного числа z = I-1
Извлекаем корни по формуле:
![]()
k = 0
![]()
![]()
или
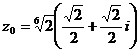
k = 1
![]()
![]()
или
![]()
k = 2
![]()
![]()
или
![]()
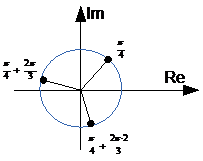
Отобразим число на комплексной оси.
![]()