Передаточная функция
По определению передаточная функция (ПФ) представляет собой оператор, равный отношению изображений выходной и входной координат при нулевых начальных условиях:Назначение сервиса. Объект управления (ОУ) описывается линейным дифференциальным уравнением n порядка. Для колебательного звена n-го порядка определяются:
- передаточная функция;
- частотные характеристики (амплитудная (АЧХ), фазовая (ФЧХ), логарифмическая (ЛЧХ));
- переходная и импульсная переходная (весовая) функции;
- графики переходных и частотных характеристик.
Пример. Объект управления (ОУ) описывается линейным дифференциальным уравнением третьего порядка:
![]() (2)
(2)
1) Передаточная функция ОУ в общем случае может быть представлена в виде отношения
W(iω) = A(ω)eiφ(ω) = U(ω) + iV(ω),
где R(p)и Q(p) – изображения по Лапласу выходной и входной переменных ОУ, соответствующих левой и правой частям уравнения 1. Отсюда, передаточная функция будет иметь вид:
![]() (3)
(3)
или
![]() . (4)
. (4)
2) Определим частотные характеристики ОУ. Известно, что частотная передаточная функция W(ω) может быть представлена в виде:
![]() , (5)
, (5)
где A(ω) – амплитудная частотная характеристика (АЧХ);
φ(ω) – фазовая частотная характеристика (ФЧХ);
U(ω) – вещественная частотная характеристика (ВЧХ);
V(ω) – мнимая частотная характеристика;
Подставим iω в выражение (3) вместо p. Получим:
![]() (6)
(6)
На основе выражений (5) и (6) выделим отдельно амплитудную и фазовую частотные характеристики и подставим численные значения коэффициентов. Исходя из того, что:
A(ω) = |W(iω)|
φ(ω) = arg(W(iω))
(см. комплексные числа). Окончательно получим:
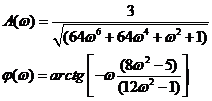 (7)
(7)
3) Определим логарифмическую амплитудную частотную характеристику (ЛАЧХ).
Известно, что ЛАЧХ определяется из соотношения:
L(ω) = 20lg(A(ω)) (8)
Данная характеристика имеет размерность дБ (децибелы) и показывает изменение отношения мощностей выходной величины к входной. Для удобства ЛАЧХ строят в логарифмическом масштабе.
Фазовая частотная характеристика, построенная в логарифмическом масштабе, будет называться логарифмической фазовой частотной характеристикой (ЛФЧХ).
Примеры построения ЛАЧХ и ЛФЧХ для наших исходных данных приведены на рисунке 1.
Определим импульсную переходную (весовую) функцию. Весовая функция w(t) представляет собой реакцию системы на единичную импульсную функцию, поданную на ее вход. Весовая функция связана с передаточной функцией преобразованием Лапласа.
![]() . (9)
. (9)
Следовательно, весовую функцию можно найти, применив обратное преобразование Лапласа к передаточной функции.
w(t) = L-1[W(p)] (10)
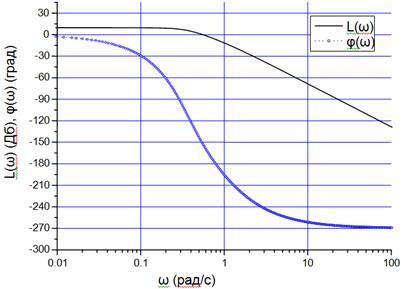
Рисунок 1 - L(ω) – ЛАЧХ системы (Дб); φ(ω) – ЛФЧХ системы (град); ω – частота входного сигнала (рад/с)
Вычислим приближенно корни полиномов R(p) и Q(p), а затем найдем обратное преобразование Лапласа от передаточной функции и построим график весовой функции (рисунок 2). Весовая функция является производной от переходной функции h(t), которая является реакцией системы на ступенчатое воздействие. Проинтегрировав w(t) или выполнив обратное преобразование Лапласа над W(p)/p, найдем переходную функцию h(t) и построим соответствующий график (рисунок 3).
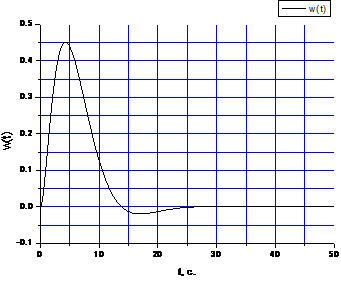
Рисунок 2 - Временные характеристики. Импульсная переходная функция w(t)
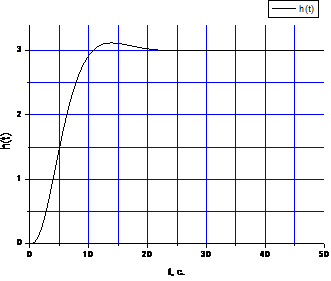
Рисунок 3 - Переходная функция h(t)

