Таблица интегралов
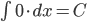
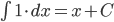
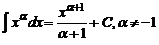, например, ∫x2dx = x2+1/(2+1)+C = x3/3+C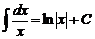
; 
; 
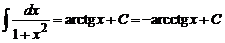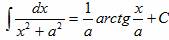
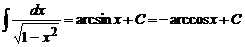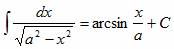
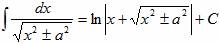
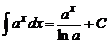
∫exdx = ex+C∫cos(x)dx = sin(x)+C∫sin(x)dx = -cos(x)+C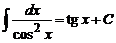
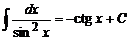
∫sh(x)dx = ch(x)+C∫ch(x)dx = sh(x)+C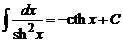
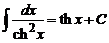
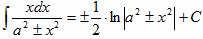
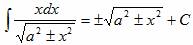
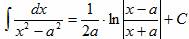
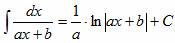
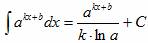
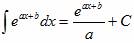
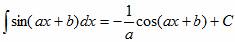
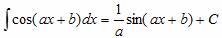
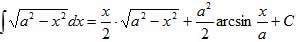
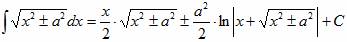
Решение интегралов
Примечание: число "пи" (π) записывается как pi; знак "бесконечность" (∞) ≡ infinity
Примеры правильной записи некоторых выражений
см. также справочник: М.Л. Смолянский Примеры правильной записи некоторых выражений
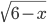 | sqrt(6-x) |
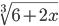 | (6+2*x)^(1/3) |
| log5(1+x) | log(1+x,5) |
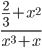 | (2/3+x^2)/(x^3+x) |
Таблицы неопределенных интегралов. Дополнительные таблицы неопределенных интегралов можно найти здесь:
Таблицы неопределенных интегралов. Брычков Ю.А., Маричев О.И., Прудников А.П. 2-е изд., исправ. — М.: ФИЗМАТЛИТ, 2003
Свойства неопределенного интеграла
- d∫f(x)dx = f(x)dx;
- ∫dF(x) = F(x)+C;
- ∫a·f(x)dx = a·∫f(x)dx;
- ∫(f(x) ± g(x))dx = ∫f(x)dx ± ∫g(x)dx;
- ∫f(x)dx = ∫f(x(t))·x′(t)dt.
Используя свойства 1-5 и свойства дифференциалов, сводят вычисление интегралов к так называемым табличным интегралам. Таблица интегралов обратна к таблице производных и может быть легко получена.