Задача о назначениях
Назначение сервиса. С помощью данного онлайн калькулятора можно:- найти путь с минимальной стоимостью назначения и с максимальной стоимостью назначения, решить задачу о назначении венгерским методом (методом Куна), решить задачу о назначении методом потенциалов;
- найти оптимальное использование рабочих агентов;
Инструкция. Выберите размерность матрицы (количество вакансий и количество кандидатов). После ввода данных, создается шаблон решения в Excel (см. задача о назначениях в Excel).
Типичное задание:
В цехе предприятия имеются 5 универсальных станков, которые могут выполнять 4 вида работ. Каждую работу единовременно может выполнять только один станок, и каждый станок можно загружать только одной работой.
В таблице даны затраты времени при выполнении станком определённой работы. Определить наиболее рациональное распределение работ между станками, минимизирующее суммарные затраты времени.
Задача. Служба занятости имеет в наличии четыре вакантных места по разным специальностям, на которые претендуют шесть человек. Проведено тестирование претендентов, результаты которого в виде баллов представлены в матрице
Распределить претендентов на вакантные места таким образом, чтобы на каждое место был назначен человек с наибольшим набранным по тестированию баллом.
Пример решения задачи о назначении с минимальной стоимостью;
Пример решения задачи о назначении с максимальной стоимостью;
Постановка задачи о назначениях
Сделаем содержательную постановку задачи. В объединении находится n автомобилей, способных каждый перевозить в месяц Qi тонн груза (i = 1,2,…,n). С их помощью необходимо обеспечить перевозку грузов (пиломатериал, шурупы и т.д.) от поставщиков к потребителям по n маршрутам в количестве Rj тонн в месяц (j = 1,2,…,n).Распределить автомобили по маршрутам так, чтобы минимизировать суммарную величину неиспользуемой провозной способности. Конкретизируем задачу (рис. 1). Пусть имеется 4 автомобиля и 4 маршрута. Характеристики провозных способностей автомобилей соответственно равны Q1 = 30 т., Q2 = 35 т., Q3 = 5 т., Q4 = 5 т. Характеристики потребностей потребителей соответственно равны R1 = 25 т., R2 = 32 т., R3 = 5 т., R4 = 4 т. Задача заключается в том, чтобы перевезти все грузы с минимальными издержками, для этого надо каждый автомобиль пустить по одному и только его маршруту. Понятно, если возможность автомобиля в перевозке груза ниже потребности потребителя этого груза, то на данный маршрут автомобиль не может быть назначен. Поэтому составим матрицу С, характеризующую издержки i-го автомобиля, в случае, если он будет назначен на j-й маршрут. Элементы маршрута будут равны:
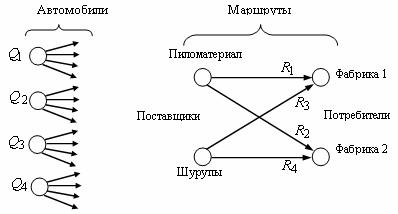
В таблице 1 приводятся оценки возможных транспортных издержек.
Таблица 1 - Оценки транспортных издержек
Rj Qi |
25 |
32 |
5 |
4 |
30 |
5 |
М |
25 |
26 |
35 |
10 |
3 |
30 |
31 |
5 |
М |
М |
0 |
1 |
5 |
М |
М |
0 |
1 |
Переменные. В качестве переменной введем величину

Ограничения. Каждый автомобиль i должен быть назначен только один раз на любой из маршрутов.
На каждый маршрут j должен быть назначен один из автомобилей
Целевая функция. В качестве целевой функции, подлежащей минимизации, выступают суммарные издержки на перевозку.
Модель задачи о назначениях примет вид:
при ограничениях:
Все предполагаемые алгоритмы поиска решения задачи о назначениях базируются на следующем утверждении: оптимальное решение задачи не изменится, если к любой строке или столбцу матрицы издержек прибавить (или вычесть) постоянную величину в силу того, что приоритет назначения не изменится. И весь алгоритм ведется на матрице издержек с соответствующими преобразованиями для получения в ней нулевых элементов, образующих систему так называемых «независимых нулей». Число независимых нулей равно размерности матрицы, а их расположение таково, что каждый из них встречается один раз в строке и один раз в столбце. Если такие независимые нули будут найдены, то в матрице решения в соответствии с их положением будут проставлены единицы. В матрице 1 нулевые элементы получены вычитанием наименьшего элемента в каждой строке.
Как только будут получены нулевые элементы, применяют различные алгоритмы: Мака, венгерский, минимальных линий. Рассмотрим процедуру вычеркивания нулевых элементов минимальным числом прямых линий. В матрице 2 показано, как используется это правило. Могут быть и другие варианты вычеркивания.
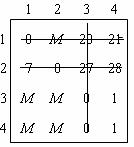
Если все нулевые элементы в матрице будут вычеркнуты, а минимальное число линий будет равно размерности матрицы, то независимые нули в матрице существуют, и решение найдено. В противном случае выбирается наименьший элемент из невычеркнутых элементов (он равен 1). Этот элемент вычитается из каждого невычеркнутого элемента и прибавляется к каждому элементу, стоящему на пересечении проведенных прямых.
В результате получается матрица (3), которая указывает на два оптимальных решения (матрицы решений 4 и 5).
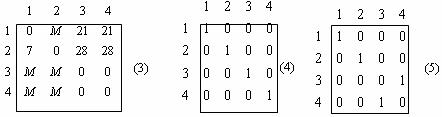
Значение целевой Z = 5 + 3 + 0 + 1 = 9 . Оптимальное решение можно было получить и сразу, не применяя процедуру вычеркивания нулей, если в матрице 2 из столбца 4 вычесть минимальный элемент. Сделано было иначе только для демонстрации процедуры вычеркивания.
Следует заметить, что, если на последнем шаге оптимальное решение не достигнуто, то процедуру проведения прямых следует повторять до тех пор, пока не будет получено допустимое решение.
Модель назначений
Модель назначений часто встречается в задачах управления, где требуется, например, распределить мастеров-ремонтников по вызовам, продавщиц по отделам, аудиторов по фирмам и т. д. В качестве примера рассмотрим возможную постановку задачи назначения.Пример. Руководство фирмы приняло решение произвести инспекцию своих предприятий в Лейпциге, Нанси, Льеже и Тилбурге, направляя туда своих вице-президентов, каждый из которых в компании возглавляет одно из направлений (финансы, маркетинг, производство и персонал). Хотя может существовать большое число факторов, которые нужно учесть при таком назначении (знание языка, узкая специализация, невозможность оторваться от прямых обязанностей и т. д.), руководство компании решило оптимизировать в качестве первого шага только суммарные затраты на командировку вице-президентов. Таблица командировочных расходов в различные города (тыс. долларов) приведена ниже.
| Вице-президенты | Лейпциг | Нанси | Льеж | Тилбург |
По финансам | 24 | 10 | 21 | 11 |
По маркетингу | 14 | 22 | 10 | 15 |
По производству | 15 | 17 | 20 | 19 |
По персоналу | 11 | 19 | 14 |
Требуется составить схему распределения вице-президентов по филиалам, минимизирующую командировочные расходы.
Решение. Табличная модель этой задачи после проведенной оптимизации приведена на рис.
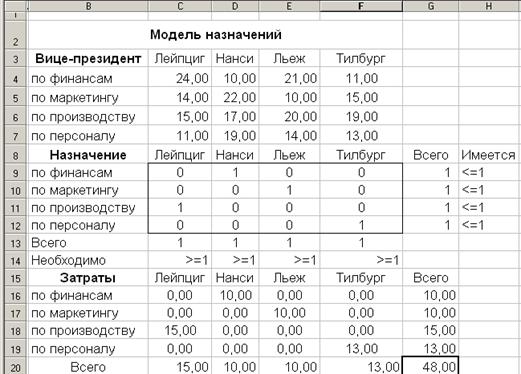
Модель назначений является разновидностью транспортной модели. От последней она отличается только тем, что в ней единица предложения не может распределяться по нескольким местам назначения (ср. рис.).
Таким образом, модель назначений всегда можно построить в виде транспортной модели, в которой предложение в каждой исходной точке и спрос в каждом конечном пункте равны единице.
Точно так же, как и транспортная модель, модель назначений может быть несбалансированной, содержать недопустимые назначения, иметь альтернативные решения при одном и том же значении целевой функции. Эти варианты моделей назначения строятся в полной аналогии с соответствующими транспортными моделями.
Оптимальное распределение продавцов по торговым точкам
Задание. Существует 4 продавца А1, А2, А3, А4 и 4 торговые точки В1, В2, В3, В4. Эффективность работы продавцов на торговых точках задаётся следующей матрицей:| 9 | 3 | 4 | 8 |
| 4 | 6 | 7 | 11 |
| 5 | 8 | 8 | 4 |
| 6 | 12 | 15 | 9 |
Найти оптимальное распределение продавцов по торговым точкам.
Поскольку задана матрица эффективности, то искать необходимо максимальные значения, следовательно, целевая функция стремится к максимуму. Именно поэтому при решении выбираем вид Максимальная прибыль.
Модифицируем матрицу умножением всех элементов на (-1) и затем сложением их с максимальным элементом матрицы (15) так, чтобы матрица не содержала бы отрицательных элементов:
| 6 | 12 | 11 | 7 |
| 11 | 9 | 8 | 4 |
| 10 | 7 | 7 | 11 |
| 9 | 3 | 0 | 6 |
1. Проводим редукцию матрицы по строкам. В связи с этим во вновь полученной матрице в каждой строке будет как минимум один ноль.
| 0 | 6 | 5 | 1 | 6 |
| 7 | 5 | 4 | 0 | 4 |
| 3 | 0 | 0 | 4 | 7 |
| 9 | 3 | 0 | 6 | 0 |
| 0 | 6 | 5 | 1 |
| 7 | 5 | 4 | 0 |
| 3 | 0 | 0 | 4 |
| 9 | 3 | 0 | 6 |
| 0 | 0 | 0 | 0 |
2. Методом проб и ошибок проводим поиск допустимого решения, для которого все назначения имеют нулевую стоимость.
Фиксируем нулевое значение в клетке (1, 1). Другие нули в строке 1 и столбце 1 вычеркиваем.
Фиксируем нулевое значение в клетке (2, 4). Другие нули в строке 2 и столбце 4 вычеркиваем.
Фиксируем нулевое значение в клетке (3, 2). Другие нули в строке 3 и столбце 2 вычеркиваем.
Фиксируем нулевое значение в клетке (4, 3). Другие нули в строке 4 и столбце 3 вычеркиваем.
В итоге получаем следующую матрицу:
| [0] | 6 | 5 | 1 |
| 7 | 5 | 4 | [0] |
| 3 | [0] | [-0-] | 4 |
| 9 | 3 | [0] | 6 |
| 0 | 6 | 5 | 1 |
| 7 | 5 | 4 | 0 |
| 3 | 0 | 0 | 4 |
| 9 | 3 | 0 | 6 |
| [0] | 6 | 5 | 1 |
| 7 | 5 | 4 | [0] |
| 3 | [0] | [-0-] | 4 |
| 9 | 3 | [0] | 6 |
Cmax = 9 + 11 + 8 + 15 = 43
Таким образом, распределение продавцов по торговым точкам будет следующее:
1 продавец – торговая точка №1
2 продавец – торговая точка №4
3 продавец – торговая точка №2
4 продавец – торговая точка №3.
При таком назначении, максимальная эффективность составит 43.


