Оптимальное использование рабочих агентов
Торговая фирма продает товары в n различных городах, покупательная способность жителей которых оценивается bj усл. ед., j = 1,…,n. Для реализации товаров фирма располагает n торговыми агентами, каждого из которых она направляет в один из городов. Профессиональный уровень агентов различен; доля реализуемых i-м торговым агентом покупательных способностей составляет аi, i = 1,…,n. Как следует распределить торговых агентов по городам, чтобы фирма получила максимальную выручку от продажи товаров?Решение этой проблемы может быть найдено с помощью задачи о назначениях. В качестве кандидатов выступают торговые агенты, в качестве работ – города.
Введем параметр сij = ai bj , характеризующий величину покупательных способностей, реализуемых i-м торговым агентом в j-м городе.
Управляющие переменные xij , i = 1,…,n; j = 1,…,n определяются по формуле
xij = 1, если i-й агент направлен в j-й город;
xij = M, в противном случае.
Математическая модель запишется в следующей форме:
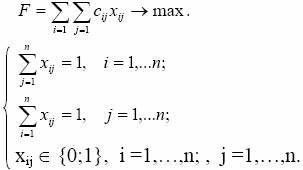
Первое и второе ограничения формализуют соответственно условия о том, что в каждый город направляется один торговый агент и один торговый агент не может работать в двух городах. Целевая функция F – это сумма реализованных покупательных способностей всеми торговыми агентами во всех городах. Она должна подлежать максимизации. Для решения задачи венгерским методом надо, как и в предыдущем примере, перейти к противоположной функции.
Перейти к решению задачи о назначениях


