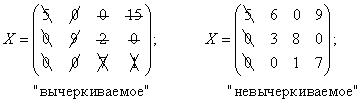Методы построения начального опорного решения
Метод Северо-западного угла используют для нахождения произвольного опорного плана транспортной задачи.Схема метода: 1) Полагают верхний левый элемент матрицы X
x 11 = min(a 1 ,b1)
Возможны три случая:
а)если a1 < b1, то х11=а1 и всю первую строку начиная со второго элемента заполняют нулями.
б)если a1 > b1, то Х11=b1, а все оставшиеся элементы первого столбца заполняют нулями.
в)если a1 = b1, то х11 = a 1 = b 1 , и все оставшиеся элементы первых столбца и строки заполняют нулями.
На этом один шаг метода заканчивается.
2) Пусть уже проделано к шагов, кm-й шаг состоит в следующем.
Определяют верхний левый элемент незаполненной части матрицы X. Пусть это элемент хl, m.
Тогда полагают хl,m = min(аkl, bkm),
где
аkl = al - Σxlj
bkm = bm - Σxim
Если аkl < bkm, то заполняют нулями l -ю строку начиная с (m + 1)-го элемента. В противном случае заполняют нулями оставшуюся часть m-го столбца.
Метод минимального элемента позволяет построить начальный опорный план транспортной задачи и является вариантом метода северозападного угла,
учитывающим специфику матрицы С=(cij)m,n. В отличие от метода северо-западного угла данный метод позволяет сразу получить достаточно экономичный план и сокращает общее количество итераций по его оптимизации.
Схема метода: элементы матрицы С нумеруют начиная от минимального в порядке возрастания, а затем в этом же порядке заполняют матрицу Х0.
Пусть элементом с минимальным порядковым номером оказался элемент x0ij .
Тогда полагают x 0 ij = min (ai, bj)
Возможны три случая:
а) если min (ai, bj) = ai, то оставшуюся часть i-й строки заполняют нулями;
б) если min (a1, b1) = bj, то оставшуюся часть j-ro столбца заполняют нулями.
в) если ai = bj, то оставшуюся часть строки и столбца заполняют нулями.
Далее этот процесс повторяют с незаполненной частью матрицы.
Пусть элементом с k -м порядковым номером оказался хklm.
Тогда хklm = min(akl, bkm),
где
а k l = al - Σxglj, g = 1..l-1
bkm = bm - Σxuim, u = 1..k-1
Возможны три случая:
а) аkl < bkm, тогда хklm = аkl и оставшуюся часть строки l заполняют нулями;
б) аkl > bkm, тогда хklm = bkm и остаток столбца m заполняют нулями;
в) аk = bkm, тогда оставшуюся часть строки l и столбца m заполняют нулями.
Метод северо-западного угла.
Существует ряд методов построения начального опорного решения, наиболее простым из которых является метод северо-западного угла. В данном методе запасы очередного поставщика используются для обеспечения запросов очередных потребителей до тех пор, пока не будут исчерпаны полностью, после чего используются запасы следующего по номеру поставщика.Заполнение таблицы транспортной задачи начинается с левого верхнего угла и состоит из ряда однотипных шагов. На каждом шаге, исходя из запасов очередного поставщика и запросов очередного потребителя, заполняется только одна клетка и соответственно исключается из рассмотрения один поставщик или потребитель. Осуществляется это таким образом:
1) если ai< b j то х ij = аi, и исключается поставщик с номером i,
xim = 0, m = 1, 2, ..., n , m ≠j, bj’=bj- ai
2) если ai> b j то х ij = bj, и исключается потребитель с номером j, xmj= 0, m= 1,2, ..., k, m≠i, ai‘= ai - bj,
3) если a i = bj то хij= ai= bj, исключается либо поставщик i, xim= 0, m= 1,2, ..., n, m≠j, , bj’=0 , либо j-й потребитель, xmj= 0, m= 1,2, ..., k, m≠i, ai‘= 0.
Нулевые перевозки принято заносить в таблицу только тогда, когда они попадают в клетку (i, j), подлежащую заполнению. Если в очередную клетку таблицы (i, j) требуется поставить перевозку, а i-й поставщик или j-й потребитель имеет нулевые запасы или запросы, то в клетку ставится перевозка, равная нулю (базисный нуль), и после этого, как обычно, исключается из рассмотрения соответствующий поставщик или потребитель. Таким образом, в таблицу заносят только базисные нули, остальные клетки с нулевыми перевозками остаются пустыми.
Во избежание ошибок после построения начального опорного решения необходимо проверить, что число занятых клеток равно k+ n- 1 и векторы-условия, соответствующие этим клеткам линейно независимы.
□ Теорема. Решение транспортной задачи, построенное методом северо-западного угла, является опорным.
Доказательство . Число занятых опорным решением клеток таблицы должно быть равно N = k+ n-1. На каждом шаге построения решения по методу северо-западного угла заполняется одна клетка и исключается из рассмотрения одна строка (поставщик) или один столбец (потребитель) таблицы задачи. Через k+ n– 2 шага в таблице будет занято k+ n– 2 клетки. В то же время останутся невычеркнуты-ми одна строка и один столбец, при этом незанятая клетка одна. При заполнении этой последней клетки число занятых клеток составит
k + n - 2 +1= k + n– 1.
Проверим, что векторы, соответствующие занятым опорным решением клеткам, линейно независимы. Применим метод вычеркивания. Все занятые клетки можно вычеркнуть, если проделать это в порядке их заполнения. ■
Необходимо иметь в виду, что метод северо-западного угла не учитывает стоимость перевозок, поэтому опорное решение, построенное данным методом, может быть далеко от оптимального.
Пример. Составить начальное опорное решение, используя метод северо-западного угла, для транспортной задачи, исходные данные которой представлены в следующей таблице
|
ai bj |
150 |
200 |
100 |
100 |
|
100 |
1 |
3 |
4 |
2 |
|
250 |
4 |
5 |
8 |
3 |
|
200 |
2 |
3 |
6 |
7 |
Решение. Распределяем запасы 1-го поставщика. Так как его запасы a 1 = 100 меньше запросов 1-го потребителя b1 = 150, то в клетку (1, 1) записываем перевозку х11 = 100 и исключаем из рассмотрения 1-го поставщика. Определяем оставшиеся неудовлетворенными запросы 1-го потребителя b’ = b1— а1 = 150 - 100 = 50.
Распределяем запасы 2-го поставщика. Так как его запасы а2 = 250 больше оставшихся неудовлетворенными запросов 1-го потребителя b1’= 50, то в клетку (2, 1) записываем перевозку х21= 50 и исключаем из рассмотрения 1-го потребителя. Определяем оставшиеся запасы 2-го поставщика а2 = а2— b1’ = 250 -50=200. Т.к. а2‘= b2=200, то в клетку (2, 2) записываем х22= 200 и исключаем по своему усмотрению либо 2-го поставщика, либо 2-го потребителя. Пусть исключили 2-го поставщика. Вычисляем оставшиеся неудовлетворенными запросы 2-го потребителя b2'= b2- а2' = 200 - 200 = 0.
Распределяем запасы 3-го поставщика. Так как а3 > b2(200 > 0), то в клетку (3, 2) записываем х32 = 0 и исключаем 2-го потребителя. Запасы 3-го поставщика не изменились a3’=a3-b2’=200 - 0 = 200. Сравниваем а3' и b3(200 > 100), в клетку (3, 3) записываем х33 = 100, исключаем 3-го потребителя и вычисляем а3" = а3'-b3= 200 - 100 = 100. Так как a3'' = b4, то в клетку (3, 4) записываем х34 = 100. Ввиду того, что задача с правильным балансом, запасы всех поставщиков исчерпаны и запросы всех потребителей удовлетворены полностью и одновременно.
Результаты построения опорного решения приведены в таблице:
|
|
150 |
200 |
100 |
100 |
|
100 |
100 |
|
|
|
|
250 |
50 |
200 |
|
|
|
200 |
|
0 |
100 |
100 |
Проверяем правильность построения опорного решения. Число занятых клеток должно быть равно N = k +n — 1 = 3 + 4— 1=6 . В нашей таблице занято шесть клеток. Применяя метод вычеркивания, убеждаемся, что найденное решение является «вычеркиваемым»:
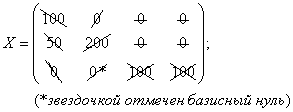
Следовательно, векторы-условия, соответствующие занятым клеткам, линейно независимы и построенное решение является опорным.
Метод минимальной стоимости
Метод минимальной стоимости прост, он позволяет построить опорное решение, достаточно близкое к оптимальному, так как использует матрицу стоимостей транспортной задачи C={cij}, i=1,2, ..., k, j=1,2, ..., n. Как и метод северо-западного угла, он состоит из ряда однотипных шагов, на каждом из которых заполняется только одна клетка таблицы, соответствующая минимальной стоимости min {с ij}}, и исключается из рассмотрения только одна строка (поставщик) или один столбец (потребитель). Очередную клетку, соответствующую min {с ij}, заполняют по тем же правилам, что и в методе северо-западного угла. Поставщик исключается из рассмотрения, если его запасы использованы полностью. Потребитель исключается из рассмотрения, если его запросы удовлетворены полностью. На каждом шаге исключается либо один поставщик, либо один потребитель. При этом если поставщик, еще не исключен, но его запасы равны нулю, то на том шаге, когда oт данного поставщика требуется поставить груз, в соответствующую клетку таблицы заносится базисный нуль и лишь затем поставщик исключается из рассмотрения. Аналогично с потребителем.□ Теорема. Решение транспортной задачи, построенное методом минимальной стоимости, является опорным. ■
Доказательство аналогично доказательству предыдущей теоремы.
Пример. Используя метод минимальной стоимости, построить начальное опорное решение транспортной задачи, исходные данные которой приведены в таблице:
|
|
4 0 |
6 0 |
8 0 |
6 0 |
|
60 |
1 |
3 |
4 |
2 |
|
80 |
4 |
5 |
8 |
3 |
|
100 |
2 |
3 |
6 |
7 |
Решение . Запишем отдельно матрицу стоимостей для того, чтобы удобнее было выбирать минимальные стоимости, вычеркивать строки и столбцы:
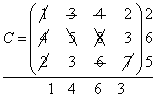
Среди элементов матрицы стоимостей выбираем наименьшую стоимость с11 = 1, отмечаем ее кружочком. Это стоимость перевозки груза от 1-го поставщика 1-му потребителю. В соответствующую клетку (1, 1) записываем максимально возможный объем перевозки х11 = min {a,, A,} = min {60, 40} =40.
Таблица 6.6
|
|
40 |
60 |
80 |
60 |
|
60 |
40 |
|
|
20 |
|
80 |
|
|
40 |
40 |
|
100 |
|
60 |
40 |
|
Запасы 1-го поставщика уменьшаем на 40, т.е. a 1 ’= a1 -b1= 60 - 40.= = 20. Исключаем из рассмотрения 1-го потребителя, так как его запросы удовлетворены. В матрице, С вычеркиваем 1-й столбец.
В оставшейся части матрицы С минимальной является стоимость с14 = 2. Максимально возможная перевозка, которую можно осуществить от 1 -го поставщика к 4-му потребителю, равна x14=min{a1’,b4}= min{20,60} = 20. В соответствующую клетку таблицы записываем перевозку х14=20- Запасы 1-гo поставщика исчерпаны, исключаем его из рассмотрения. В матрице С вычёркиваем первую строку. Запросы 4-го потребителя уменьшаем на 20, т.е. b4' = b4- a1'=60-20= 40.
В оставшейся части матрицы С минимальная стоимость с24=с32=3. Заполняем одну из двух клеток таблицы (2, 4) или (3, 2). Пусть в клетку (2, 4) записываем х24 = min{а2, b 4 } = min {80, 40} = 40 . Запросы 4-го потребителя удовлетворены, исключаем его из рассмотрения» вычеркиваем четвертый столбец в матрице С. Уменьшаем запасы 2-го поставщика а2’ = а2 - b 4 = 80 - 40 = 40 .
В оставшейся части матрицы С минимальная стоимость min{сij} = с32 = 3. Записываем в клетку таблицы (3,2) перевозку х32=min {а3 b2} = min {100, 60} = 60. Исключаем из рассмотрения 2-го потребителя, а из матрицы С второй столбец. Вычисляем а3’= а3-b2 = 100 — 60 = 40.
В оставшейся части матрицы С минимальная стоимость min {сij}= с33 = 6. Записываем в клетку таблицы (3,3) перевозку x33 = min {а3',b3} = min {40, 80} = 40. Исключаем из рассмотрения 3-го поставщика, а из матрицы С третью строку. Определяем b3' = b3— а3' = 80 — 40 = 40.
В матрице С остается единственный элемент с23 = 8. Записываем в клетку таблицы (2, 3) перевозку х23 = 40.
Проверяем правильность построения опорного решения. Число занятых клеток таблицы равно N = k+ n- 1=3+4-1=6. Методом вычеркивания проверяем линейную независимость векторов-условий, соответствующих положительным координатам решения. Порядок вычеркивания показан на матрице X:
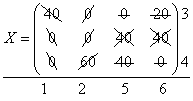
Решение является «вычеркиваемым» и, следовательно, опорным.
Переход от одного опорного решения к другому
В транспортной задаче переход от одного опорного решения к другому осуществляется с помощью цикла. Для некоторой свободной клетки таблицы строится цикл, содержащий часть клеток, занятых опорным решением. По этому циклу перераспределяются объемы перевозок. Перевозка загружается в выбранную свободную клетку и освобождается одна из занятых клеток, получается новое опорное решение.□ Теорема (о существовании и единственности цикла). Если таблица транспортной задачи содержит опорное решение, то для любой свободной клетки таблицы существует единственный цикл, содержащий эту клетку и часть клеток, занятых опорным решением.
Доказательство . Опорное решение занимает N = k + n- 1 клеток таблицы, которым соответствуют линейно независимые векторы-условия. Согласно доказанной выше теореме ни одна часть занятых клеток не образует цикл. Если же к занятым клеткам присоединить одну свободную, то соответствующие им k+ n векторов линейно зависимы, и по той же теореме существует цикл, содержащий эту клетку. Предположим, что таких циклов два (i1,j1), (i1,j2), (i2,j2),…, (i k ,j1), и (i1,j1), (i2,j1), (i2,j2),…, (i l ,j1), -Тогда, объединив клетки обоих циклов без свободной клетки (i1,j1), получим последовательность клеток (i1,j1), (i1,j2), (i2,j2),…, (i k ,j1), (i1,j1), (i2,j1), (i2,j2),…, (i l ,j1) которые образуют цикл. Это противоречит линейной независимости векторов-условий, образующих базис опорного решения. Следовательно, такой цикл единственный.
Означенный цикл.
Цикл называется означенным, если его угловые клетки пронумерованы по порядку и нечетным клеткам приписан знак «+», а четным — знак «-».
Сдвигом по циклу на величину θ называется увеличение объемов перевозок во всех нечетных клетках цикла, отмеченных знаком «+», на θ и уменьшение объемов перевозок во всех четных клетках, отмеченных знаком «-», на θ.
□ Теорема. Если таблица транспортной задачи содержит опорное решение, то при сдвиге по любому циклу, содержащему одну свободную клетку, на величину
получится опорное решение.
Доказательство . В таблице транспортной задачи, содержащей опорное решение, выберем свободную клетку и отметим ее знаком «+». По теореме 6.6 для этой клетки существует единственный цикл, который содержит часть клеток, занятых опорным решением. Пронумеруем клетки цикла, начиная с клетки, отмеченной знаком - «+». Найдем
осуществим сдвиг по циклу на эту величину
В каждой строке и в каждом столбце таблицы, входящих в цикл, две и только две клетки, одна из которых отмечена знаком «+», а другая — знаком «-». Поэтому в одной клетке объем перевозки увеличивается на θ, а в другой уменьшается на θ, при этом сумма всех перевозок в строке (или столбце) таблицы остается неизменной. Следовательно , после сдвига по циклу по-прежнему и запасы всех поставщиков вывозятся полностью, и запросы всех потребителей удовлетворяются полностью. Так как сдвиг по циклу осуществляется на величину
все объемы перевозок будут неотрицательными. Следовательно, новое решение является допустимым.
Если оставить свободной одну из клеток с нулевым объемом перевозки, соответствующих
, то число занятых клеток будет равно N=k+n-1. Одна клетка загружается (отмеченная знаком «+»), одна — освобождается. Так как цикл единственный, то удаление из него одной клетки разрывает его. Цикл из оставшихся занятых клеток образовать нельзя, соответствующие векторы-условия линейно независимы, а решение является опорным.
Метод вычеркивания
Метод вычеркивания позволяет проверить, является ли данное решение транспортной задачи опорным.Пусть допустимое решение транспортной задачи, которое имеет k + n - 1 отличную от нуля координату, записано в таблицу. Чтобы данное решение было опорным, векторы-условия, соответствующие положительным координатам, должны быть линейно независимыми. Для этого занятые решением клетки таблицы должны быть расположены так, чтобы из них нельзя было образовать цикл.
Строка или столбец таблицы с одной занятой клеткой не может входить в какой-либо цикл, так как цикл имеет две и только две клетки в каждой строке или в столбце. Следовательно, можно вычеркнуть сначала либо все строки таблицы, содержащие по одной занятой клетке, либо все столбцы, содержащие по одной занятой клетке, далее, вернуться к столбцам (строкам) и продолжить их вычеркивание. Если в результате вычеркиваний все строки и столбцы будут вычеркнуты, значит, из занятых клеток таблицы нельзя выделить часть, образующую цикл, и система соответствующих векторов-условий линейно независима, а решение является опорным. Если же после вычеркиваний останется часть клеток, то эти клетки образуют цикл, система соответствующих векторов-условий линейно зависима, а решение не является опорным.
Ниже приведены примеры «вычеркиваемого» (опорного) и «невычеркиваемого» (неопорного) решений;
