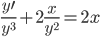Основные теоремы теории вероятностей
1. Бросается игральная кость один раз. Найдите вероятность выпадения грани с тремя или пятью очками.Решение. Пусть событие A — появление грани с тремя очками, событие B — с пятью очками.
и 
. События A и B несовместные, так как появление грани с тремя очками исключает появление грани с пятью очками и наоборот.
Поэтому
.
2. Найдите вероятность того, что наудачу взятое двузначное число окажется кратным либо 2, либо 5, либо тому и другому одновременно.
Решение. Пусть событие A означает, что наудачу взятое двузначное число кратно 2. Событие B — двузначное число кратно 5. Найдем P(A+B). Так как события A и B совместные, то P(A+B) = P(A)+ P(B) - P (A · B). Двузначные числа — это числа 10, 11, 12, . .., 99. Всего их 90. Из них 45 будут кратны 2, 18 кратны 5 и 9 кратны 2 и 5 одновременно. Поэтому 
; 
; 
.
Следовательно, 
.
3. Имеются две урны с шарами. В одной 10 красных и 5 синих шаров, во второй 5 красных и 7 синих шаров. Какова вероятность того, что из первой урны наудачу будет вынут красный шар, а из второй синий?
Решение. Пусть событие A1— из первой урны вынут красный шар; A2— из второй урны вынут синий шар:
, 
.
События A1 и A2 независимые. Вероятность совместного появления событий A1 и A2 равна
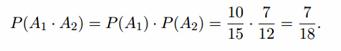
4. Имеется колода карт (36 штук). Вынимаются наудачу две карты подряд. Какова вероятность того, что обе вынутые карты будут красной масти?
Решение. Пусть событие A1 — первая вынутая карта красной масти. Событие A2 - вторая вынутая карта красной масти. B — обе вынутые карты красной масти. Так как должны произойти и событие A1, и событие A2 , то B = A1 · A2. События A1 и A2 зависимые, следовательно, P (B) вычисляем по формуле (9).
Отсюда
5. В двух урнах находятся шары, отличающиеся только цветом, причем в первой урне 5 белых шаров, 11 черных и 8 красных, а во второй соответственно 10, 8, 6 шаров. Из обеих урн наудачу извлекается по одному шару. Какова вероятность, что оба шара одного цвета?
Решение. Пусть индекс 1 означает белый цвет, индекс 2 — черный цвет; 3 — красный цвет. Пусть событие Ai — из первой урны извлекли шар i-го цвета; событие Bj — из второй урны извлекли шар j -го цвета; событие A — оба шара одного цвета.
A = A1 · B1 + A2 · B2 + A3 · B3. События Ai и Bj независимые, а Ai · Bi и Aj · Bj несовместные при i ≠ j . Следовательно,
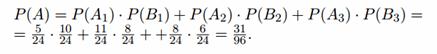
6. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что взятое изделие стандартное, равна 0,9. Найдите вероятность того, что из двух проверенных изделий только одно стандартное.
Решение. Пусть событие Ai — i-е изделие стандартное, i = 1; 2. Пусть событие A — из двух проверенных изделий только одно стандартное. 
— тоже независимые события; события 
и 
— несовместные события.
7. Одновременно произвели выстрел 4 пушки. Вероятность того, что в цель попаданий, с первого орудия равна 0,6, с другой - 0,65, с третьей - 0,75, с четвертой - 0,7. Найти вероятность того, что в цель:
а) не попаданий;
б) попаданий только из двух пушек.
Решение.
а) не попаданий;
P(0) = (1-0.6)*(1-0.65)*(1-0.75)*(1-0.7) = 0.0105
б) попаданий только из двух пушек.
P(2) = 0.6*0.65*(1-0.75)*(1-0.7) + 0.6*(1-0.65)*(1-0.75)*0.7 + (1-0.6)*(1-0.65)*0.75*0.7 + (1-0.6)*0.65*0.75*(1-0.7) = 0.198