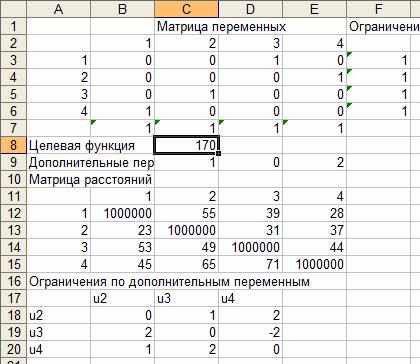
Решение задачи коммивояжера в Excel
Алгоритм решения задачи коммивояжера в Excel
- Формирование шаблона через сервис
- Открыть шаблон в Excel и выполнить команду Сервис / Поиск решения
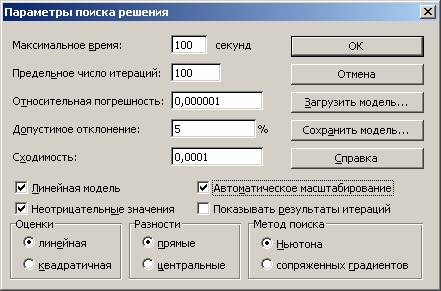
- Установка параметров
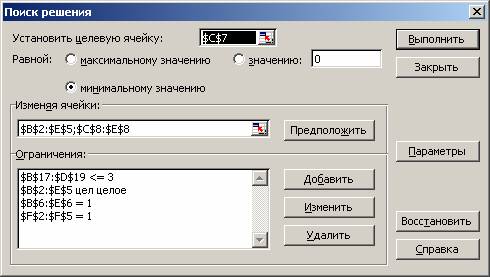
- Установка ограничений
Ограничения дополнительных переменных "≤ n - 2"
где n - размерность матрицы
Пример. Коммивояжеру, находящемуся в городе А, необходимо посетить три города – B, C и D. Он получил информацию о стоимости перелета в каждый из выбранных городов из города А и стоимости перелета из одного города в другой. На основании полученных данных он составил матрицу стоимостей (см. таблицу) перелета в выбранные города и обратно.
Требуется так составить маршрут поездки, чтобы затраты на дорогу были минимальными и чтобы каждый пункт посещался только один раз.
| Города | №1 | №2 | №3 | №4 |
| №1 | 0 | 55 | 39 | 28 |
| №2 | 23 | 0 | 31 | 37 |
| №3 | 53 | 49 | 0 | 44 |
| №4 | 45 | 65 | 71 | 0 |
Математическая модель
Определим булевы переменные задачи:xij = 1, если коммивояжер переезжает из города i в город j;
xij = 0, если коммивояжер не переезжает из города i в город j.
Тогда задача заключается в определении минимума целевой функции:
,
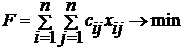выражающей минимальную длину маршрута, при ограничениях:
, j = 1,2,…,n - коммивояжер может въехать в город j только один раз,
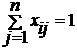, i= 1,2,…,n - коммивояжер может выехать из города i только один раз.
В задаче коммивояжера в число ограничений необходимо ввести еще одну систему условий:
ui - uj + (n-l) ∙ xij ≤ n-2, i≠j, i,j = 2,..., n,
которые обеспечивают устранение распадения единого маршрута на несколько не связанных между собой (частичных) маршрутов, а также предотвращают образование циклов, означающих перемещение коммивояжера по замкнутому частичному маршруту.
Задача коммивояжера также относится к классу транспортных задач с дополнительными условиями на целостность и замкнутость маршрута.
Решение задачи коммивояжера в EXCEL
Имеется 5 городов, расстояния cij между которыми приведены в таблице:| Города | №1 | №2 | №3 | №4 |
| №1 | ∞ | 55 | 39 | 28 |
| №2 | 23 | ∞ | 31 | 37 |
| №3 | 53 | 49 | ∞ | 44 |
| №4 | 45 | 65 | 71 | ∞ |
В диагональные клетки таблицы занесены символы ∞, предотвращающие зацикливание маршрута на одном городе. На практике вместо символа ∞ заносится любое большое число (в данном примере число 1000000), значительно превосходящее остальные числа в таблице.
Коммивояжер, выезжая из города №1, должен посетить все города, побывав в каждом из них только один раз, и вернуться в исходный город №1.
Необходимо определить такой маршрут объезда городов, для которого длина маршрута будет минимальной.
Математическая модель
Переменные xij могут принимать значения, равные либо 0, либо 1. Целевая функция равна:
ограничения имеют вид:
- условие въезда в город j только один раз,
- условие выезда в город j только один раз,
ui- uj+3∙xij≤ 3, i≠j, i,j=2,3,4.
Задание исходных данных и ограничений
Задание исходных данных в рабочей книге Excel приведено в табл. 1-5. В этих же таблицах приведены формулы для вычисления ограничений и целевой функции.Таблица 1
Задание ограничений на решение задачи
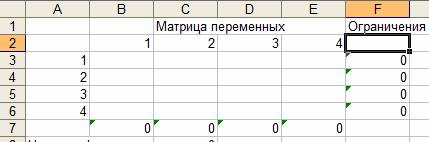
Таблица 2
Задание матрицы расстояний между городами
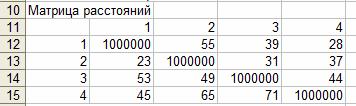
Таблица 3
Задание целевой функции
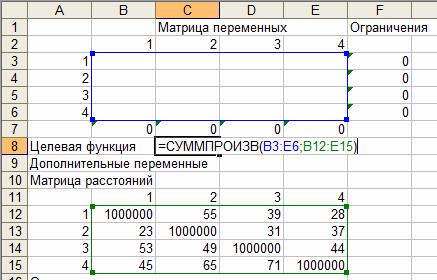
Таблица 4
Задание ячеек для дополнительных переменных ui
Таблица 5
Задание условий для дополнительных переменных
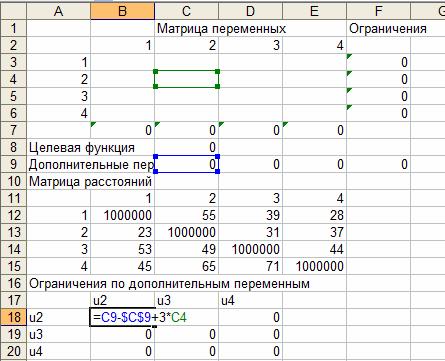
В окне Поиск решения установить следующие параметры решения задачи:
· Установить целевую ячейку - $С$8,
· равной минимальному значению.
Изменяя ячейки: $B$2:$E$5, $C$8:$E$8 - сюда заносятся не только ячейки, которые будут изменяться и в которых будут занесены решения задачи (ячейки с адресами $B$2:$E$5), но и ячейки $C$8:$E$8, содержащие переменные ui, которые также являются изменяемыми.
Ограничения задачи заносятся так же, как указано в лабораторных работах №1-№3, с обязательным указанием того, что переменные в ячейках $B$2:$E$5 - двоичные. В окне Параметры отметить: линейная модель, неотрицательные значения, автоматическое масштабирование.
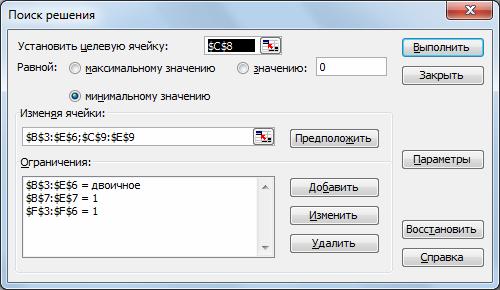
Таблица 6
