Коэффициент Фехнера
Коэффициент Фехнера - это оценка степени согласованности направлений отклонений индивидуальных значений факторного и результативного признаков от средних значений факторного и результативного признаков. Коэффициент Фехнера наряду с такими коэффициентами, как коэффициент Спирмэна и коэффициент Кэндэла, относится к коэффициентам корреляции знаков. Коэффициент корреляции знаков основан на оценке степени согласованности направлений отклонений индивидуальных значений факторного и результативного признаков от соответствующих средних. Вычисляется он следующим образом:где na - число совпадений знаков отклонений индивидуальных величин от средней; nb - число несовпадений.
Назначение сервиса. Данный сервис предназначен для расчета коэффициент Фехнера в онлайн режиме. Также определяется значимость данного коэффициента.
Расчет коэффициента Фехнера состоит из следующих этапов:
- Определяют средние значения для каждого признака (X и Y).
- Определяют знаки отклонения (-,+) от среднего значения каждого из признаков.
- Если знаки совпадают, присваивают значение А, иначе В.
- Считают количество А и В, вычисляя коэффициент Фехнера по формуле:
Kф = (na - nb)/(na + nb) где na - число совпадений знаков отклонений индивидуальных величин от средней; nb - число несовпадений.
Свойства коэффициента Фехнера
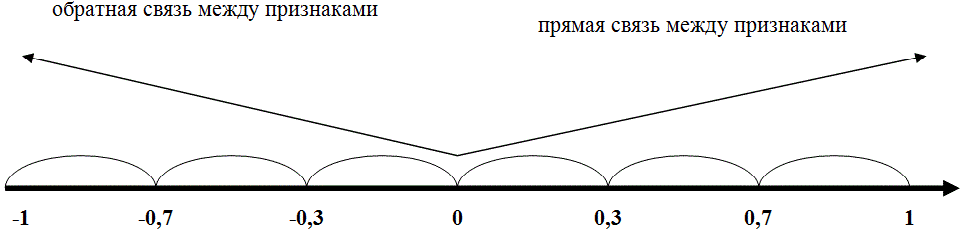
Коэффициент Фехнера изменяется в пределах [-1;+1] и применяется для оценки тесноты связи качественных признаков (непараметрические методы).| Значение коэффициента Фехнера | Качественная характеристика силы связи |
| [-0,9;-1] | Очень высокая обратная |
| [-0,7;-0,9] | Высокая обратная |
| [-0,5;-0,7] | Заметная обратная |
| [-0,3;-0,5] | Умеренная обратная |
| [-0,1;-0,3] | Слабая обратная |
| 0 | Связь отсутствует |
| 0,1 - 0,3 | Слабая прямая |
| 0,3 - 0,5 | Умеренная прямая |
| 0,5 - 0,7 | Заметная прямая |
| 0,7 - 0,9 | Высокая прямая |
| 0,9 - 1 | Очень высокая прямая |
Графическое представление коэффициента Фехнера
Пример №1. При разработке глинистого раствора с пониженной водоотдачей в высокотемпературных условиях проводили параллельное испытание двух рецептур, одна из которых содержала 2% КМЦ и 1% Na2CO3, а другая 2% КМЦ, 1% Na2CO3 и 0,1% бихромата калия. В результате получена следующие значения Х (водоотдача через 30 с).
| X1 | 9 | 9 | 11 | 9 | 8 | 11 | 10 | 8 | 10 |
| X2 | 10 | 11 | 10 | 12 | 11 | 12 | 12 | 10 | 9 |
Пример №2. Коэффициент корреляции знаков, или коэффициент Фехнера, основан на оценке степени согласованности направлений отклонений индивидуальных значений факторного и результативного признаков от соответствующих средних. Вычисляется он следующим образом:
где na - число совпадений знаков отклонений индивидуальных величин от средней; nb - число несовпадений.
Коэффициент Фехнера может принимать значения от -1 до +1. Kф = 1 свидетельствует о возможном наличии прямой связи, Kф =-1 свидетельствует о возможном наличии обратной связи.
Рассмотрим на примере расчет коэффициента Фехнера по данным, приведенным в таблице:
| Xi | Yi | Знаки отклонений значений признака от средней | Совпадение (а) или несовпадение (в) знаков | |
| Для Xi | Для Yi | |||
| 8 | 40 | - | - | А |
| 9 | 50 | - | + | В |
| 10 | 48 | - | + | В |
| 10 | 52 | - | + | В |
| 11 | 41 | + | - | В |
| 13 | 30 | + | - | В |
| 15 | 35 | + | - | В |
Для примера: ![]() .
.
Значение коэффициента свидетельствует о том, что можно предполагать наличие обратной связи.
Перейти к онлайн решению своей задачи
Пример №2
Рассмотрим на примере расчет коэффициента Фехнера по данным, приведенным в таблице:
Средние значения:
![]()
![]()
| Xi | Yi | Знаки отклонений от средней X | Знаки отклонений от средней Y | Совпадение (а) или несовпадение (b) знаков |
| 12 | 220 | + | - | B |
| 9 | 1070 | - | + | B |
| 8 | 1000 | - | + | B |
| 14 | 606 | + | - | B |
| 15 | 780 | + | + | A |
| 10 | 790 | - | + | B |
| 10 | 900 | - | + | B |
| 15 | 544 | + | - | B |
| 93 | 5910 | 0 | 0 | 0 |
![]()
Значение коэффициента свидетельствует о том, что можно предполагать наличие обратной связи.
Оценка Коэффициента корреляции знаков.
Для оценки коэффициента Фехнера достаточно оценить его значимость и найти доверительный интервал.Значимость коэффициента Фехнера.
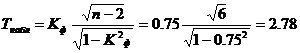
По таблице Стьюдента находим tтабл:
tтабл (n-m-1;a) = (6;0.05) = 1.943
Поскольку Tнабл > tтабл, то отклоняем гипотезу о равенстве 0 коэффициента корреляции знаков. Другими словами, коэффициент Фехнера статистически - значим.
Интервальная оценка для коэффициента корреляции знаков
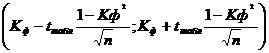
Доверительный интервал для коэффициента Фехнера:
r(-1.0;-0.4495)
Пример №3.
Рассмотрим на примере расчет коэффициента корреляции знаков по данным, приведенным в таблице:
| Xi | Yi | Знаки отклонений от средней X | Знаки отклонений от средней Y | Совпадение (а) или несовпадение (b) знаков |
| 96 | 220 | + | - | B |
| 52 | 1070 | - | + | B |
| 60 | 1000 | - | + | B |
| 89 | 606 | + | - | B |
| 82 | 780 | + | + | A |
| 77 | 790 | - | + | B |
| 70 | 900 | - | + | B |
| 92 | 544 | + | - | B |
| 618 | 5910 | 0 | 0 | 0 |
![]()
Значение коэффициента свидетельствует о том, что можно предполагать наличие обратной связи.
Оценка коэффициента корреляции знаков. Значимость коэффициента корреляции знаков.
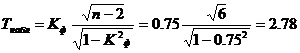
По таблице Стьюдента находим tтабл:
tтабл (n-m-1;a) = (6;0.05) = 1.943
Поскольку Tнабл > tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции знаков. Другими словами, коэффициент корреляции знаков статистически - значим.
Доверительный интервал для коэффициента корреляции знаков.
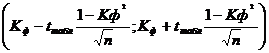
Доверительный интервал для коэффициента корреляции знаков.
r(-1;-0.4495)