Разложение в ряд Тейлора
Если функция f(x) имеет на некотором интервале, содержащем точку а, производные всех порядков, то к ней может быть применена формула Тейлора: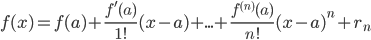 ,
,
где rn – так называемый остаточный член или остаток ряда, его можно оценить с помощью формулы Лагранжа:
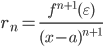 , где число x заключено между х и а.
, где число x заключено между х и а.
- Формула Тейлора
- Разложения функции в степенной ряд
- Разложение функции в ряд Тейлора в окрестности бесконечности
- Приближенные вычисления с помощью степенных рядов
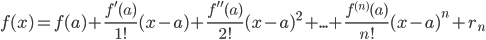
Таким образом, функция f(x) может быть разложена в ряд Тейлора в рассматриваемой точке х, если:
- она имеет производные всех порядков;
- построенный ряд сходится в этой точке.
При а=0 получаем ряд, называемый рядом Маклорена:
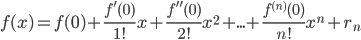
Показательные функции
Тригонометрические функции
Функция actgx не разлагается по степеням x, т.к. ctg0=∞
Гиперболические функции
Логарифмические функции
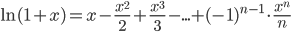 , -1<x<1, R = 1
, -1<x<1, R = 1
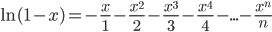
Биномиальные ряды
Пример №1. Разложить в степенной ряд функцию f(x)=2x.
Решение. Найдем значения функции и ее производных при х=0
f(x) = 2x, f(0) = 20=1;
f'(x) = 2xln2, f'(0) = 20 ln2= ln2;
f''(x) = 2x ln22, f''(0) = 20 ln22= ln22;
…
f(n)(x) = 2x lnn2, f(n)(0) = 20 lnn2= lnn2.
Подставляя полученные значения производных в формулу ряда Тейлора, получим:
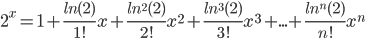
Пример №2. Написать ряд Тейлора по степеням (х+4) для функции f(x)=ex.
Решение. Находим производные функции ex и их значения в точке х=-4.
f(x) = еx, f(-4) = е-4;
f'(x) = еx, f'(-4) = е-4;
f''(x) = еx, f''(-4) = е-4;
…
f(n)(x) = еx, f(n)( -4) = е-4.
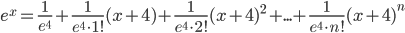
Данное разложение также справедливо для -∞<x<+∞.
Пример №3. Разложить функцию f(x)=lnx в ряд по степеням (х-1),
( т.е. в ряд Тейлора в окрестности точки х=1).
Решение. Находим производные данной функции.
f(x)=lnx, 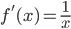 ,
, 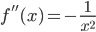 ,
, 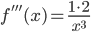 ,
, 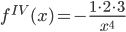
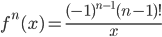
f(1)=ln1=0, f'(1)=1, f''(1)=-1, f'''(1)=1*2,..., f(n)=(-1)n-1(n-1)!
Подставляя эти значения в формулу, получим искомый ряд Тейлора:
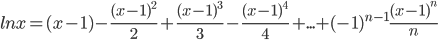
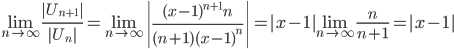
Пример №4. Разложить в степенной ряд функцию 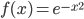 .
.
Решение. В разложении (1) заменяем х на -х2, получаем:
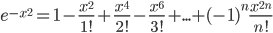 , -∞<x<∞
, -∞<x<∞Пример №5. Разложить в ряд Маклорена функцию 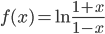 .
.
Решение. Имеем 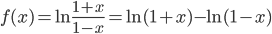
Пользуясь формулой (4), можем записать:
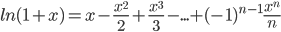
подставляя вместо х в формулу –х, получим:
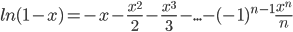
Отсюда находим: ln(1+x)-ln(1-x) = 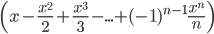 -
- 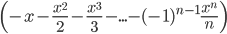
Раскрывая скобки, переставляя члены ряда и делая приведение подобных слагаемых, получим
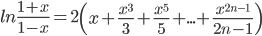 . Этот ряд сходится в интервале (-1;1), так как он получен из двух рядов, каждый из которых сходится в этом интервале.
. Этот ряд сходится в интервале (-1;1), так как он получен из двух рядов, каждый из которых сходится в этом интервале.
Разложения функции в степенной ряд
Формулами (1)-(5) можно пользоваться и для разложения соответствующих функций в ряд Тейлора, т.е. для разложения функций по целым положительным степеням (х-а). Для этого над заданной функцией необходимо произвести такие тождественные преобразования, чтобы получить одну из функций (1)-(5), в которой вместо х стоит k(х-а)m, где k – постоянное число, m – целое положительное число. Часто при этом удобно сделать замену переменной t=х-а и раскладывать полученную функцию относительно t в ряд Маклорена.Этот метод основан на теореме о единственности разложения функции в степенной ряд. Сущность этой теоремы состоит в том, что в окрестности одной и той же точки не может быть получено два различных степенных ряда, которые бы сходились к одной и той же функции, каким бы способом ее разложение ни производилось.
Пример №5а. Разложить в ряд Маклорена функцию 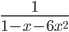 , указать область сходимости.
, указать область сходимости.
Решение. Сначала найдем 1-x-6x2=(1-3x)(1+2x), далее разложим дробь с помощью сервиса.
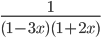 на элементарные:
на элементарные: 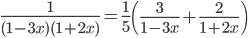
Дробь 3/(1-3x) можно рассматривать как сумму бесконечно убывающей геометрической прогрессии знаменателем 3x, если |3x| < 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд
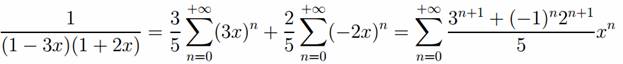
Пример №6. Разложить функцию 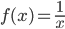 в ряд Тейлора в окрестности точки х=3.
в ряд Тейлора в окрестности точки х=3.
Решение. Эту задачу можно решить, как и раньше, с помощью определения ряда Тейлора, для чего нужно найти производные функции и их значения при х=3. Однако проще будет воспользоваться имеющимся разложением (5):
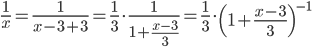 =
= 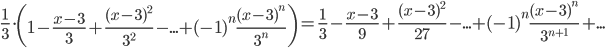
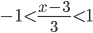 или –3<x-3<3, 0<x< 6 и является искомым рядом Тейлора для данной функции.
или –3<x-3<3, 0<x< 6 и является искомым рядом Тейлора для данной функции.
Пример №7. Написать ряд Тейлора по степеням (х-1) функции ln(x+2).
Решение.
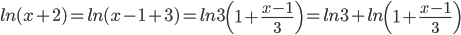
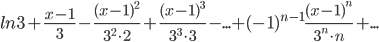
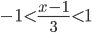 , или -2 < x < 5.
, или -2 < x < 5.
Пример №8. Разложить функцию f(x)=sin(πx/4) в ряд Тейлора в окрестности точки x=2.
Решение. Сделаем замену t=х-2:
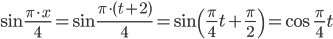
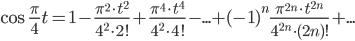
Таким образом,
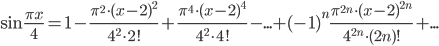 , (-∞<x<+∞)
, (-∞<x<+∞)Разложение функции в ряд Тейлора в окрестности бесконечности
Задача о разложении функции f(x) в ряд Тейлора в окрестности бесконечности ставится как задача о разложении функции g(t)=f(1/x) в окрестности t=0. Затем делается обратная замена.Пример. 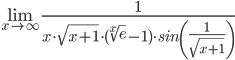
Поскольку 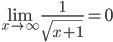 , то в силу свойств первого замечательного предела, исходное выражение можно упростить:
, то в силу свойств первого замечательного предела, исходное выражение можно упростить:
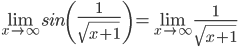
Тогда исходный предел можно представить в виде: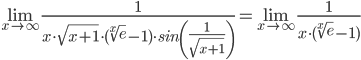
У функции exp(1/x) делаем замену аргумента на t=1/x: exp(t).
Функцию exp(t) представим в виде разложения в ряд Тейлора:
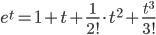 +...+
+...+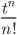
Выполним обратную замену:
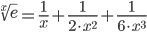
Тогда исходное выражение можно представить как: 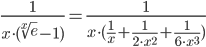
Расскроем скобки и упростим выражение: 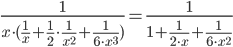
Тогда: 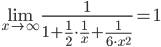
Приближенные вычисления с помощью степенных рядов
Степенные ряды широко используются в приближенных вычислениях. С их помощью с заданной точностью можно вычислять значения корней, тригонометрических функций, логарифмов чисел, определенных интегралов. Ряды применяются также при интегрировании дифференциальных уравнений.Рассмотрим разложение функции в степенной ряд:
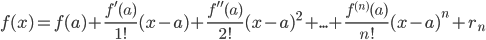
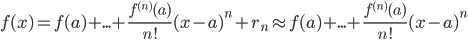
- если полученный ряд является знакочередующимся, то используется следующее свойство: для знакочередующегося ряда, удовлетворяющего условиям Лейбница, остаток ряда по абсолютной величине не превосходит первого отброшенного члена.
- если данный ряд знакопостоянный, то ряд, составленный из отброшенных членов, сравнивают с бесконечно убывающей геометрической прогрессией.
- в общем случае для оценки остатка ряда Тейлора можно воспользоваться формулой Лагранжа: a<c<x (или x<c<a).
Пример №1. Вычислить ln(3) с точностью до 0,01.
Решение. Воспользуемся разложением 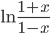 , где x=1/2 (см. пример 5 в предыдущей теме):
, где x=1/2 (см. пример 5 в предыдущей теме):
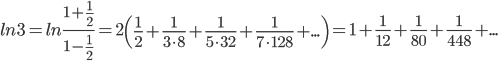
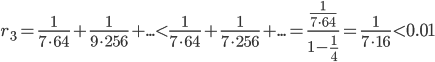
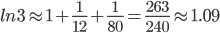
Пример №2. Вычислить 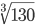 с точностью до 0,0001.
с точностью до 0,0001.
Решение. Воспользуемся биномиальным рядом. Так как 53 является ближайшим к 130 кубом целого числа, то целесообразно число 130 представить в виде 130=53+5.
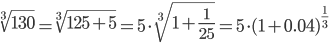
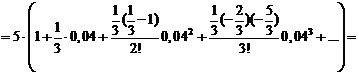
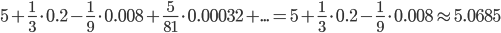
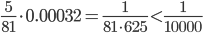 , поэтому его и следующие за ним члены можно отбросить.
, поэтому его и следующие за ним члены можно отбросить.
Многие практически нужные определенные или несобственные интегралы не могут быть вычислены с помощью формулы Ньютона-Лейбница, ибо ее применение связано с нахождением первообразной, часто не имеющей выражения в элементарных функциях. Бывает также, что нахождение первообразной возможно, но излишне трудоемко. Однако если подынтегральная функция раскладывается в степенной ряд, а пределы интегрирования принадлежат интервалу сходимости этого ряда, то возможно приближенное вычисление интеграла с наперед заданной точностью.
Пример №3. Вычислить интеграл с точностью до 10-5.
Решение. Соответствующий неопределенный интеграл 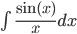 не может быть выражен в элементарных функциях, т.е. представляет собой «неберущийся интеграл». Применить формулу Ньютона-Лейбница здесь нельзя. Вычислим интеграл приближенно.
не может быть выражен в элементарных функциях, т.е. представляет собой «неберущийся интеграл». Применить формулу Ньютона-Лейбница здесь нельзя. Вычислим интеграл приближенно.
Разделив почленно ряд для sinx на x , получим:
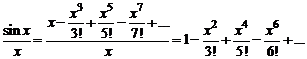
Интегрируя этот ряд почленно (это возможно, так как пределы интегрирования принадлежат интервалу сходимости данного ряда), получаем:
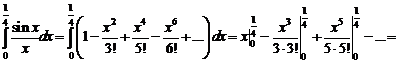
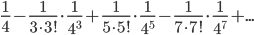
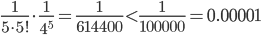 достаточно взять сумму первых двух членов, чтобы получить искомое значение с заданной точностью.
достаточно взять сумму первых двух членов, чтобы получить искомое значение с заданной точностью.
Таким образом, находим
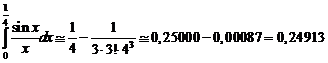
Пример №4. Вычислить интеграл с точностью до 0,001.
Решение.
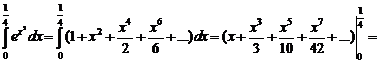
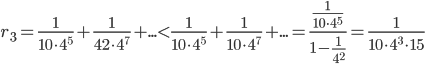 ≈0.0001<0.001
≈0.0001<0.001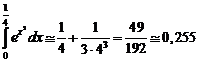 .
.