Перевод чисел в двоичную, шестнадцатеричную, десятичную, восьмеричную системы счисления
Назначение сервиса. Сервис предназначен для перевода чисел из одной системы счисления в другую в онлайн режиме. Для этого выберите основание системы, из которой необходимо перевести число. Вводить можно как целые, так и числа с запятой.- Операции с двоичными числами (сложение и вычитание)
- Умножение двоичных чисел
- Формат представления чисел с плавающей запятой
Пример №1. Представить число 133,54 в форме числа с плавающей точкой.
Решение. Представим число 133.54 в нормализованном экспоненциальном виде:
1.3354*102 = 1.3354*exp102
Число 1.3354*exp102 состоит из двух частей: мантиссы M=1.3354 и экспоненты exp10=2
Если мантисса находится в диапазоне 1 ≤ M < 10, то число считается нормализованным.
Представление числа в денормализованном экспоненциальном виде.
Если мантисса находится в диапазоне 0,1 ≤ M < 1, то число считается денормализованным.
Представим число в денормализованном экспоненциальном виде: 0.13354*exp103Пример №2. Представить двоичное число 101.102 в нормализованном виде, записать в 32-битом стандарте IEEE754.
- Таблица истинности
- Алгебра и геометрия







Способы представления чисел
Двоичные (binary) числа – каждая цифра означает значение одного бита (0 или 1), старший бит всегда пишется слева, после числа ставится буква «b». Для удобства восприятия тетрады могут быть разделены пробелами. Например, 1010 0101b.Шестнадцатеричные (hexadecimal) числа – каждая тетрада представляется одним символом 0...9, А, В, ..., F. Обозначаться такое представление может по-разному, здесь используется только символ «h» после последней шестнадцатеричной цифры. Например, A5h. В текстах программ это же число может обозначаться и как 0хА5, и как 0A5h, в зависимости от синтаксиса языка программирования. Незначащий ноль (0) добавляется слева от старшей шестнадцатеричной цифры, изображаемой буквой, чтобы различать числа и символические имена.
Десятичные (decimal) числа – каждый байт (слово, двойное слово) представляется обычным числом, а признак десятичного представления (букву «d») обычно опускают. Байт из предыдущих примеров имеет десятичное значение 165. В отличие от двоичной и шестнадцатеричной формы записи, по десятичной трудно в уме определить значение каждого бита, что иногда приходится делать.
Восьмеричные (octal) числа – каждая тройка бит (разделение начинается с младшего) записывается в виде цифры 0–7, в конце ставится признак «о». То же самое число будет записано как 245о. Восьмеричная система неудобна тем, что байт невозможно разделить поровну.
см. также Представление чисел в ЭВМ
Алгоритм перевода чисел из одной системы счисления в другую
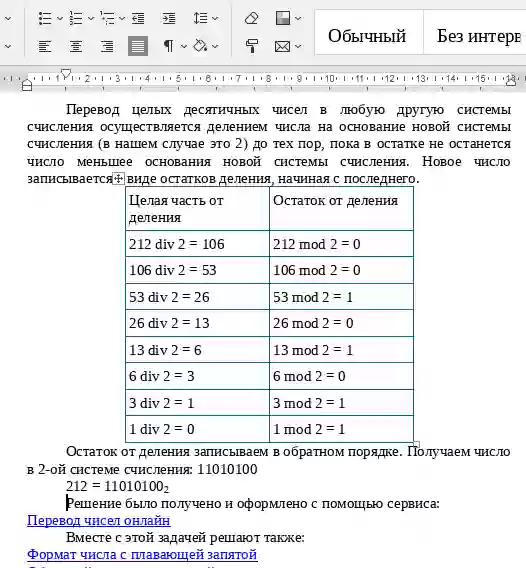
Перевод целых десятичных чисел в любую другую системы счисления осуществляется делением числа на основание новой системы счисления до тех пор, пока в остатке не останется число меньшее основания новой системы счисления. Новое число записывается в виде остатков деления, начиная с последнего.Перевод правильной десятичной дроби в другую ПСС осуществляется умножением только дробной части числа на основание новой системы счисления до тех пор пока в дробной части не останутся все нули или пока не будет достигнута заданная точность перевода. В результате выполнения каждой операции умножения формируется одна цифра нового числа начиная со старшего.
Перевод неправильной дроби осуществляется по 1 и 2 правилу. Целую и дробную часть записывают вместе, отделяя запятой.
Пример №1.
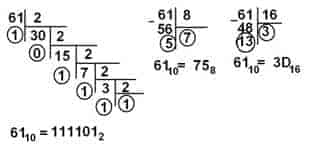
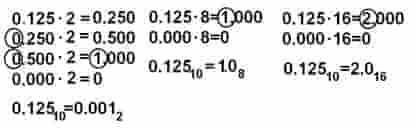
Перевод из 2 в 8 в 16 системы счисления.
Эти системы кратны двум, следовательно, перевод осуществляется с использованием таблицы соответствия (см. ниже).
Для перевода числа из двоичной системы счисления в восьмиричную (шестнадцатиричную) необходимо от запятой вправо и влево разбить двоичное число на группы по три (четыре – для шестнадцатиричной) разряда, дополняя при необходимости нулями крайние группы. Каждую группу заменяют соответствующей восьмиричной или шестнадцатиричной цифрой.
Пример №2. 1010111010,1011 = 1.010.111.010,101.1 = 1272,548
здесь 001=1; 010=2; 111=7; 010=2; 101=5; 100=4
При переводе в шестнадцатеричную систему необходимо делить число на части, по четыре цифры, соблюдая те же правила.
Пример №3. 1010111010,1011 = 10.1011.1010,1011 = 2B12,13HEX
здесь 0010=2; 1011=B; 1010=12; 1011=13
Перевод чисел из 2, 8 и 16 в десятичную систему исчисления производят путем разбивания числа на отдельные и умножения его на основание системы (из которой переводится число) возведенное в степень соответствующую его порядковому номеру в переводимом числе. При этом числа нумеруются влево от запятой (первое число имеет номер 0) с возрастанием, а в правую сторону с убыванием (т.е. с отрицательным знаком). Полученные результаты складываются.
Пример №4.
Пример перевода из двоичной в десятичную систему счисления.
1010010,1012 = 1·26+0·25+1·24+0·23+0·22+1·21+0·20 + 1·2-1+0·2-2+1·2-3 =Пример перевода из восьмеричной в десятичную систему счисления.
= 64+0+16+0+0+2+0+0.5+0+0.125 = 82.62510
108.58 = 1*·82+0·81+8·80 + 5·8-1 = 64+0+8+0.625 = 72.62510Пример перевода из шестнадцатеричной в десятичную систему счисления.
108.516 = 1·162+0·161+8·160 + 5·16-1 = 256+0+8+0.3125 = 264.312510
Еще раз повторим алгоритм перевода чисел из одной системы счисления в другую ПСС
- Из десятичной системы счисления:
- разделить число на основание переводимой системы счисления;
- найти остаток от деления целой части числа;
- записать все остатки от деления в обратном порядке;
- Из двоичной системы счисления
- Для перевода в десятичную систему счисления необходимо найти сумму произведений основания 2 на соответствующую степень разряда;
- Для перевода числа в восьмеричную необходимо разбить число на триады.
Например, 1000110 = 1 000 110 = 1068 - Для перевода числа из двоичной системы счисления в шестнадцатеричную необходимо разбить число на группы по 4 разряда.
Например, 1000110 = 100 0110 = 4616
Таблица соответствия систем счисления:
| Двоичная СС | Шестнадцатеричная СС |
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
Таблица для перевода в восьмеричную систему счисления
| Двоичная СС | Восьмеричная СС |
| 000 | 0 |
| 001 | 1 |
| 010 | 2 |
| 011 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Пример №5. Перевести число 100,12 из десятичной системы счисления в восьмеричную систему счисления и обратно. Пояснить причины расхождений.
Решение.
1 Этап. Перевод числа из десятичной системы счисления в восьмеричную систему счисления.
| Целая часть от деления | Остаток от деления |
| 100 div 8 = 12 | 100 mod 8 = 4 | 12 div 8 = 1 | 12 mod 8 = 4 | 1 div 8 = 0 | 1 mod 8 = 1 |
Остаток от деления записываем в обратном порядке. Получаем число в 8-ой системе счисления: 144
100 = 1448
Для перевода дробной части числа последовательно умножаем дробную часть на основание 8. В результате каждый раз записываем целую часть произведения.
0.12*8 = 0.96 (целая часть 0)
0.96*8 = 7.68 (целая часть 7)
0.68*8 = 5.44 (целая часть 5)
0.44*8 = 3.52 (целая часть 3)
Получаем число в 8-ой системе счисления: 0753.
0.12 = 0.7538
100,1210 = 144,07538
2 Этап. Перевод числа из десятичной системы счисления в восьмеричную систему счисления.
Обратный перевод из восьмеричной системы счислений в десятичную.
Для перевода целой части необходимо умножить разряд числа на соответствующую ему степень разряда.
144 = 82*1 + 81*4 + 80*4 = 64 + 32 + 4 = 100
Для перевода дробной части необходимо разделить разряд числа на соответствующую ему степень разряда
0753 = 8-1*0 + 8-2*7 + 8-3*5 + 8-4*3 = 0.119873046875 = 0.1199
144,07538 = 100,119910 ≈ 100,1210
Разница в 0,0001 (100,12 - 100,1199) объясняется погрешностью округлений при переводе в восьмеричную систему счислений. Эту погрешность можно уменьшить, если взять большее число разрядов (например, не 4, а 8).