Сложение двоичных чисел
Назначение сервиса. Онлайн-калькулятор предназначен для сложения двоичных чисел в прямом, обратном и дополнительном кодах.Перевод чисел в двоичную, шестнадцатеричную, десятичную, восьмеричную системы счисления
Формат представления чисел с плавающей запятой
Пример №1. Представить число 133,54 в форме числа с плавающей точкой.
Решение. Представим число 133.54 в нормализованном экспоненциальном виде:
1.3354*102 = 1.3354*exp102
Число 1.3354*exp102 состоит из двух частей: мантиссы M=1.3354 и экспоненты exp10=2
Если мантисса находится в диапазоне 1 ≤ M < 10, то число считается нормализованным.
Представление числа в денормализованном экспоненциальном виде.
Если мантисса находится в диапазоне 0,1 ≤ M < 1, то число считается денормализованным.
Представим число в денормализованном экспоненциальном виде: 0.13354*exp103
Пример №2. Представить двоичное число 101.102 в нормализованном виде, записать в 32-битом стандарте IEEE754.
Таблица истинности
Арифметика в двоичной системе счисления
Арифметические действия в двоичной системе выполняются так же, как и в десятичной. Но, если в десятичной системе счисления перенос и заём осуществляется по десять единиц, то в двоичной - по две единицы. В таблице представлены правила сложения и вычитания в двоичной системе счисления.- При сложении в двоичной системе системе счисления двух единиц в данном разряде будет 0 и появится перенос единицы в старший разряд.
- При вычитании из нуля единицы производится заём единицы из старшего разряда, где есть 1. Единица, занятая в этом разряде, даёт две единицы в разряде, где вычисляется действие, а также по единице, во всех промежуточных разрядах.
| Сложение
0 + 0 = 0 1 + 0 = 1 0 + 1 = 1 1 + 1 = 10 |
Вычитание
0 – 0 = 0 1 – 0 = 1 1 – 1 = 0 10 – 1 = 1 |
Сложение чисел с учетом их знаков на машине представляет собой последовательность следующих действий:
- преобразование исходных чисел в указанный код;
- поразрядное сложение кодов;
- анализ полученного результата.
При выполнении операции в дополнительном (модифицированном дополнительном) коде если в результате сложения в знаковом разряде возникает единица переноса, она отбрасывается.
Операция вычитания в ЭВМ выполняется через сложение по правилу: Х-У=Х+(-У). Дальнейшие действия выполняются также как и для операции сложения.
Пример №1.
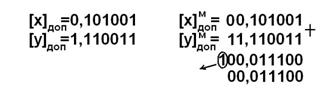
Дано: х=0,110001; y= -0,001001, сложить в обратном модифицированном коде.

Дано: х=0,101001; y= -0,001101, сложить в дополнительном модифицированном коде.
Пример №2. Решить примеры на вычитание двоичных чисел, используя метод дополнения до 1 и циклического переноса.
а) 11 - 10.
Решение.
Представим числа 112 и -102 в обратном коде.
Обратный код для положительного числа совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.
Двоичное число 0000011 имеет обратный код 0,0000011
Двоичное число 0000010 имеет обратный код 1,1111101
Сложим числа 00000011 и 11111101
В 0-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 1-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | |||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 |
В 1-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 2-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | ||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 |
В 2-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 3-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | |||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 |
В 3-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 4-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | ||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 |
В 4-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 5-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 |
В 5-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 6-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 |
В 6-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 7-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
В 7-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 8-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
В итоге получаем:
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Возник перенос из знакового разряда. Добавим его (т.е. 1) к полученному числу (тем самым осуществляя процедуру циклического переноса).
В итоге получаем:
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
Результат сложения: 00000001. Переведем в десятичное представление. Для перевода целой части необходимо умножить разряд числа на соответствующую ему степень разряда.
00000001 = 27*0 + 26*0 + 25*0 + 24*0 + 23*0 + 22*0 + 21*0 + 20*1 = 0 + 0 + 0 + 0 + 0 + 0 + 0 + 1 = 1
Результат сложения (в десятичном представлении): 1
б) 111-010
Представим числа 1112 и -0102 в обратном коде.
Обратный код для положительного числа совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.
Двоичное число 0000111 имеет обратный код 0,0000111
Двоичное число 0000010 имеет обратный код 1,1111101
Сложим числа 00000111 и 11111101
В 0-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 1-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | |||||||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 |
В 1-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 2-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | ||||||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 |
В 2-ом разряде возникло переполнение (1 + 1 + 1 = 11). Поэтому записываем 1, а 1 переносим на 3-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | |||||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 |
В 3-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 4-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | ||||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 |
В 4-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 5-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | |||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 |
В 5-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 6-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | ||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 |
В 6-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 7-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 |
В 7-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 8-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
В итоге получаем:
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
Возник перенос из знакового разряда. Добавим его (т.е. 1) к полученному числу (тем самым осуществляя процедуру циклического переноса).
В итоге получаем:
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
Результат сложения: 00000101
Получили число 00000101. Для перевода целой части необходимо умножить разряд числа на соответствующую ему степень разряда.
00000101 = 27*0 + 26*0 + 25*0 + 24*0 + 23*0 + 22*1 + 21*0 + 20*1 = 0 + 0 + 0 + 0 + 0 + 4 + 0 + 1 = 5
Результат сложения (в десятичном представлении): 5
Сложение двоичных вещественных чисел с плавающей запятой
В компьютере любое число может быть представлено в формате с плавающей точкой. Формат с плавающей точкой показан на рисунке: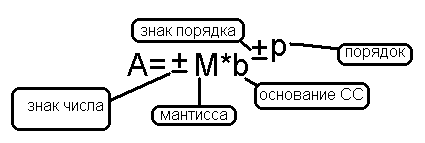
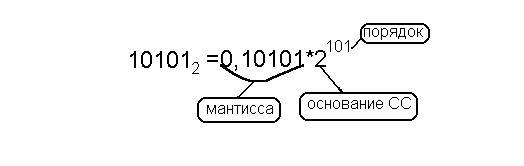
b-1≤|M|<b0=1
Нормализованное число - это число, у которого после запятой идет значащая цифра (т.е. 1 в двоичной системе счисления). Пример нормализации:
0,00101*2100=0,101*210
111,1001*210=0,111001*2101
0,01101*2-11=0,1101*2-100
11,1011*2-101=0,11011*2-11
При сложении чисел с плавающей точкой выравнивание порядков выполняют в сторону большего порядка:
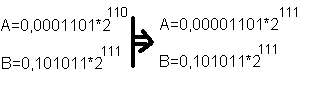
Алгоритм сложения чисел с плавающей точкой:
- Выравнивание порядков;
- Сложение мантисс в дополнительном модифицированном коде;
- Нормализация результата.
Пример №4.
A=0,1011*210, B=0,0001*211
1. Выравнивание порядков;
A=0,01011*211, B=0,0001*211
2. Сложение мантисс в дополнительном модифицированном коде;
MAдоп.мод.=00,01011
MBдоп.мод.=00,0001
00,01011
+ 00,00010
=
00,01101
A+B=0,01101*211
3. Нормализация результата.
A+B=0,1101*210
Пример №3. Записать десятичное число в двоично-десятичной системе счисления и сложить два числа в двоичной системе счисления.





