Симплекс-метод с естественным базисом
Для применения симплекс-метода с естественным базисом КЗЛП должна содержать единичную подматрицу размером mxm – в этом случае очевиден начальный опорный план (неотрицательное базисное решение системы ограничений КЗЛП).Для определенности предположим, что первые m векторов матрицы системы уравнений составляют единичную матрицу. Тогда первоначальный опорный план очевиден – (b1, b2 ,…, bm ,0,…,0).
Проверка на оптимальность опорного плана проходит с помощью признака оптимальности, переход к другому опорному плану проводится с помощью преобразований Жордана-Гаусса при использовании математического признака оптимальности. Полученный опорный план снова проверяется на оптимальность и так далее. Процесс заканчивается за конечное число шагов, причем на последнем шаге либо выявляется неразрешимость задачи (конечного оптимума нет), либо получается оптимальный опорный план и соответствующее ему оптимальное значение ЦФ.
Математический признак оптимальности состоит из следующих двух теорем:
1. Если для всех векторов А1, А2,…, Аn выполняется условие
где 
,
то полученный опорный план является оптимальным.
2. Если для некоторого вектора, не входящего в базис, выполняется условие
, то можно получить новый опорный план, для которого значение ЦФ будет больше исходного, при этом могут быть два случая:
- если все компоненты вектора, подлежащего вводу в базис, неположительны, то ЗЛП не имеет решения (конечного оптимума нет);
- если имеется хотя бы одна положительная компонента у вектора, подлежащего вводу в базис, то можно получить новый опорный план.
На основании признака оптимальности в базис вводится вектор Ак, давший минимальную отрицательную величину симплекс разности:
Чтобы выполнялось условие неотрицательности значений опорного плана, выводится из базиса вектор Аr, который дает минимальное положительное оценочное отношение
Строка Аr называется направляющей, столбец Аки элементar к– направляющими.
Элементы направляющей строки в новой симплекс-таблице вычисляются по формулам:
а элементы i-й строки – по формулам:
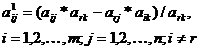
Значения нового опорного плана рассчитываются по формулам:
для i = r ;
Процесс решения продолжают либо до получения оптимального плана, либо до установления неограниченности ЦФ. Если среди симплекс-разностей (оценок) оптимального плана нулевые только оценки, соответствующие базисным векторам, то это говорит о единственности оптимального плана. Если же нулевая оценка соответствует вектору, не входящему, то в общем случае это означает, что оптимальный план не единственный.
Примечание. Для использования приведенной процедуры к минимизации линейной функции f (x1,x2,…, xn) следует искать максимум - f (x1,x2,…, xn), затем полученный максимум взять с противоположным знаком. Оптимальное решение то же.
Пример. Получить решение по модели:
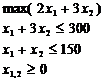
Эта задача (модель) линейного программирования, приведем ее к каноническому виду путем введения дополнительных переменных x 3 и x4:
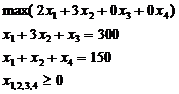
КЗЛП имеет необходимое число единичных столбцов, т.е. обладает очевидным начальным опорным планом (0,0,300,150). Решение осуществляется симплекс-методом с естественным базисом с оформлением расчетов в симплекс-таблицах:
Номер | 
| В | 2 | 3 | 0 | 0 | ||
симплекс- | Базис | план | 
| 
| 
| 
| Q | |
таблицы | 
| |||||||
А3 | 0 | 300 | 1 | 3 | 1 | 0 | 100 | |
| 0 | А4 | 0 | 150 | 1 | 1 | 0 | 1 | 150 |
f(x) | 0 | -2 | -3 | 0 | 0 | 
| ||
А2 | 3 | 100 | 1/3 | 1 | 1/3 | 0 | 300 | |
| I | А4 | 0 | 50 | 2/3 | 0 | -1/3 | 1 | 75 |
f(x) | 300 | -1 | 0 | 1 | 0 | 
| ||
А2 | 3 | 75 | 0 | 1 | 1/2 | -1/2 | ||
| II | А1 | 2 | 75 | 1 | 0 | -1/2 | 3/2 | |
f(x) | 375 | 0 | 0 | 1/2 | 3/2 |
|
В симплекс-таблице II получен оптимальный опорный план, поскольку все симплекс-разности (оценки)
j. Оптимальные значения переменных равны: x1*=75, x2* =75 (основные переменные), x3* =0, x4* =0 (дополнительные переменные). Максимальное значение целевой функции равно 375.
Таким образом, в рассмотренной выше задаче об оптимальном использовании ограниченных ресурсов, оптимальная производственная программа состоит в выпуске 75ед. изделий первого вида и 75ед. изделий второго вида. С этой программой связана максимальная выручка от реализации готовой продукции – 375 у.е.
