Несимметричные двойственные задачи в линейном программировании
Любой задаче линейного программирования (исходной) можно поставить в соответствие другую задачу, которая называется двойственной или сопряженной. Обе задачи образуют пару двойственных задач. Каждая из задач является двойственной к другой задаче рассматриваемой пары.Пусть математическая модель исходной задачи имеет вид:
Z(X)=c1x1+c2x2+…+cnxn→max
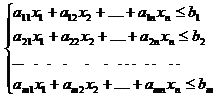
xi≥0; i=1,2,…n
Запишем ее в матричном виде:
Z(X)=CX→ max,
AX≤B,
X≥0
Правило построения двойственной задачи
- Во всех ограничениях исходной задачи свободные члены должны находиться в правой части, а члены с неизвестными – в левой.
- Ограничения-неравенства исходной задачи должны быть записаны так, чтобы знаки неравенств у них были направлены в одну сторону.
- Если знаки неравенств в исходной задаче «≥», то целевая функция должна максимизироваться, т.е. Z(X)→ max, а если «≤», то минимизироваться.
- Каждому ограничению исходной задачи соответствует неизвестное двойственной задачи; так неравенству ai1x1+ai2x2+…+ainxn≤bi
соответствует yi≥0 (i=1,2…,m).
- Каждому неизвестному исходной задачи соответствует ограничение двойственной задачи. Таким образом, количество неизвестных одной задачи соответствует числу ограничений другой.
- Матрица коэффициентов системы ограничений двойственной задачи есть транспонированная матрица коэффициентов системы ограничений исходной задачи.
- Целевая функция двойственной задачи имеет вид: F(Y)=b1y1+b2y2+…+bmym, где y1,y2,…,ym - неизвестные в двойственной задаче, b1,b2,…bm - свободные члены в ограничениях исходной задачи.
- Целевая функция F(Y) двойственной задачи должна оптимизироваться противоположным образом по сравнению с Z(X), т.е. если Z(X)→max, то F(Y) →min и наоборот.
В теории двойственности используются четыре пары двойственных задач (приведем их в матричной форме записи):
Исходная задача Двойственная задача
Симметричные пары
| 1.
| Z(X) = CX→max, AX ≤ B, X ≥ 0 | F(Y) = YB→min, YAT ≥ C, Y ≥ 0. |
| 2. | Z(X) = CX→min, AX ≥ B, X ≥ 0 | F(Y) = YB→max, YAT ≤ C, Y ≥ 0. |
Несимметричные пары
| 3. | Z(X) = CX→max,
AX = B, X ≥ 0 | F(Y) = YB→min,
YAT ≥ C, Y – любого знака |
| 4. | Z(X) = CX→min,
AX = B, X ≥ 0 | F(Y) = YB→max,
YAT ≤ C, Y – любого знака |
Здесь С = (с1,c2,…cn), Y = (y1,y2,…ym),
, 
.
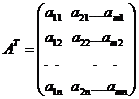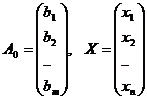Пример. Составить задачу, двойственную к данной.
Z(X) = x1+4x2+3x3→min
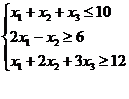
xj ≥ 0
Решение: Приведем систему ограничений к одному знаку неравенств:
,
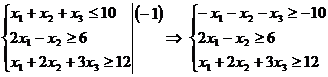Ведем переменные двойственной задачи
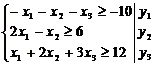
Умножим правые части ограничений на соответствующие переменные двойственной задачи и сложим их, получим целевую функцию, которая максимизируется, поскольку целевая функция исходной задачи минимизировалась: F(Y)=-10y1+6y2+12y3→max.
Умножаем коэффициенты при x1 на соответствующие переменные двойственной задачи и складываем их. Данная сумма меньше или равна коэффициенту при x1 в целевой функции –y1+2y2+y3≤1. Аналогично составляются еще два ограничения двойственной задачи.
Получена двойственная задача, составляющая с исходной симметричную пару:
F(Y)=-10y1+6y2+12y3→max
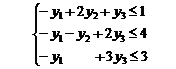yi ≥ 0; i = 1,2,3.
