Нахождение решения задачи параметрического программирования
В задачах параметрического программирования целевая функция или функции ограничений либо и то, и другое зависят от некоторых параметров.Решение задачи, целевая функция которой содержит параметр. Считая значение параметра t равным некоторому числу t0∈[α, β], находим симплексным методом или методом искусственного базиса решение полученной таким образом задачи линейного программирования.
В результате при данном значении t0 либо найдем оптимальный план задачи (1)-(3), либо установим ее неразрешимость. В первом случае, используя элементы (m+1)-й строки последней симплекс-таблицы решения задачи, в которой записаны числа Δj(t0)=Δ’j+t0Δ’’jt, находим:
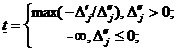 (16)
(16)
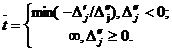 (17)
(17)
Для всех t≤t≤t задача (1)-(3) имеет один и тот же оптимальный план, что и при t0.
В том случае, если задача (1)-(3) при t0 неразрешима, в (m+1)-й строке последней симплекс-таблицы ее решения имеется число Δk= Δ’k+t0Δ’’k<0, xik≤0(i=1,m). Тогда:
1) если Δ’’k=0, то задача (1)-(3) неразрешима для любого t;
2) если Δ’’k<0, то задача (1)-(3) неразрешима для всех t<t1=-Δ’k/Δ’’k;
3) если Δ’’k>0, то задача (1)-(3) неразрешима для всех t>t1.
Определив все значения параметра t∈[α, β], для которых задача (1)-(3) имеет один и тот же оптимальный план или для которых задача неразрешима, получаем промежуток изменения параметра t, который исключаем из рассмотрения. Снова полагаем значение параметра t равным некоторому числу, принадлежащему промежутку [α,β], и находим решение полученной задачи.
После каждой итерации определяется либо промежуток, в котором для всех значений параметра задача имеет один и тот же оптимальный план, либо промежуток, в котором для всех значений параметра задача не имеет решения.
Итак, процесс нахождения решения задачи (1)-(3) включает следующие этапы:
10. Считая значение параметра t равным некоторому числу t0∈[α, β], находим оптимальный план X* или устанавливают неразрешимость полученной задачи линейного программирования.
20. Определяют множество значений параметра t∈[α, β], для которых найденный оптимальный план является оптимальным или задача неразрешима. Эти значения параметра исключают из рассмотрения.
30. Полагают значение параметра t равным некоторому числу, принадлежащему оставшейся части промежутка [α,β], и находят решение полученной задачи линейного программирования.
40. Определяют множество значений параметра t, для которых новый оптимальный план остается оптимальным или задача неразрешима. Вычисления повторяют до тех пор, пока не будут исследованы все значения параметра t∈[α, β].
Задача 2. Предприятие для изготовления различных изделий А,В и С использует три вида сырья. Норма расхода сырья каждого вида на производство единицы продукции данного вида приведена в табл. 1.21. В ней же указана цена изделия каждого вида.
Таблица 1.21
| Вид сырья | Норма затрат сырья (кг) на единицу продукции | ||
| А | В | С | |
| 1 | 18 | 15 | 12 |
| 2 | 6 | 4 | 8 |
| 3 | 5 | 3 | 3 |
| Цена единицы продукции (руб.) | 9 | 10 | 16 |
Изделия А,В и С могут производиться в любых соотношениях (сбыт обеспечен). Однако производство ограничено имеющимся в распоряжении предприятия сырьем 1 вида в количестве 360 кг, 2 вида - в количестве 192 кг, 3 вида - в количестве 180 кг.
Найти план производства изделий, реализация которого обеспечивает максимальный выпуск продукции в стоимостном выражении. Одновременно с этим провести анализ устойчивости оптимального плана задачи при условиях возможного изменения цены единицы каждого из изделий.
Решение. Составим математическую модель задачи. Обозначим планируемый выпуск изделий вида А через х1, изделий вида В - через х2, изделий вида С - через х3. Тогда математическая постановка задачи составит в определении максимального значения функции
F=9x1+10x2+16x3 (19)
при условиях
18x1+15x2+12x3≤360, (21)
6x1+4x2+8x3≤192
5x1+3x2+3x3≤180
x1,x2,x3≥0. (20)
Найдем решение задачи (19)-(20) симплексным методом. Оно приведено в таблице 1.22.
Таблица 1.22
| i | Базис | Сб | Ро | 9 | 10 | 16 | 0 | 0 | 0 |
| P1 | Р2 | Р3 | Р4 | P5 | Р6 | ||||
| 1 | Р2 | 10 | 8 | 1 | 1 | 0 | 1/9 | -1/6 | 0 |
| 2 | Р3 | 16 | 20 | 1/4 | 0 | 1 | -1/18 | 5/24 | 0 |
| 3 | Р6 | 0 | 96 | 5/4 | 0 | 0 | -1/6 | -1/8 | 1 |
| 4 | 400 | 5 | 0 | 0 | 2/9 | 5/3 | 0 |
Установим теперь возможные границы изменения цен каждого из изделий, внутри которых найденный оптимальный план производства продукции не меняется. Начнем с изделия вида А. Предположим, что его цена с1 равна не 9 руб., a 9+t1 руб., где t1 некоторый параметр. Тогда требуется найти такие значения параметра t1, что для найденного плана X*=(0,8,20) достигается максимальное значение функции
F=(9+t1)x1+10x2+16x3
при условиях (19) и (20). Чтобы сделать это, будем считать с1=9+t1 и с учетом этого составим таблицу 1.23, в которой первые три строки возьмем из табл. 1.22, а четвертую строку вычислим по правилам
Таблица 1.23
| i | Базис | сб | Ро | 9+t1 | 10 | 16 | 0 | 0 | 0 |
| P1 | Р2 | Р3 | Р4 | Р5 | Р6 | ||||
| 1 | Р2 | 10 | 8 | 1 | 1 | 0 | 1/9 | -1/6 | 0 |
| 2 | Р3 | 16 | 20 | 1/4 | 0 | 1 | -1/18 | 5/24 | 0 |
| 3 | Р6 | 0 | 96 | 5/4 | 0 | 0 | -1/6 | -1/8 | 0 |
| 4 | 400 | 5-t1 | 0 | 0 | 2/9 | 5/3 | 0 | ||
Аналогично можно показать, что если цена с2 одного изделия вида В изменяется от 8 до 20 руб., то оптимальным планом производства продукции является план, согласно которому изготовляются 8 изделий вида В и 20 изделий вида С. Отметим, что при изменении цены одного изделия вида В мы считаем постоянными все остальные исходные данные задачи. Одновременно с этим заметим, что хотя указанный план и остается оптимальным, значение целевой функции при разных значениях с2 не одинаковы. Наконец, аналогично показывается, что если цена с3 одного изделия вида С изменяется от 8 до 20 руб., то оптимальным планом производства продукции также является план, согласно которому производится 8 изделий вида В и 20 изделий вида С.
Мы провели анализ чувствительности оптимального плана задачи (18)-(20) при возможном изменении цены каждого из изделий. Аналогично можно провести анализ чувствительности оптимального плана этой задачи при одновременном изменении значений нескольких коэффициентов целевой функции.
Решение задачи, правые части ограничений которой содержат параметр. Алгоритм решения задачи (4)-(6) подобен рассмотренному выше алгоритму решения задачи (1)-(3).
Полагая значение параметра t равным некоторому числу t0, находим решение полученной задачи линейного программирования (4)-(6). При данном значении параметра t0 либо определяем оптимальный план, либо устанавливаем неразрешимость задачи. В первом случае найденный план является оптимальным для любого t≤t≤t ,где
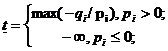
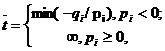
и числа qi, pi определены компонентами оптимального плана и зависят от t0:
хi*= qi+t0Pi.
Если при t=t0 задача (4)-(6) неразрешима, то либо целевая функция (4) не ограничена на множестве планов, либо система уравнений (5) не имеет неотрицательных решений. В первом случае задача неразрешима для всех t∈[α, β], а во втором случае определяем все значения параметра t∈[α, β], для которых система уравнений (5) несовместна, и исключаем их из рассмотрения.
После определения промежутка, в котором задача (4)-(6) имеет один и тот же оптимальный план или неразрешима, выбираем новое значение параметра t, не принадлежащее найденному промежутку, и находим решение полученной задачи линейного программирования. При этом решение новой задачи ищем с помощью двойственного симплекс-метода. Продолжая итерационный процесс, после конечного числа шагов получаем решение задачи (4)-(6).
Итак, процесс нахождения решения задачи (4)-(6) включает следующие основные этапы:
10. Считая значение параметра t равным некоторому числу t0∈[α, β], находят оптимальный план или устанавливают неразрешимость полученной задачи линейного программирования.
20. Находят значение параметра t∈[α, β], для которых задача (4)-(6) имеет один и тот же оптимальный план или неразрешима. Эти значения параметра t исключают из рассмотрения.
30. Выбирают значение параметра t из оставшейся части промежутка [α,β] и устанавливают возможность определения нового оптимального плана. В случае существования оптимального плана находят его двойственным симплекс-методом.
40. Определяют множество значений параметра t, для которых задача имеет один и тот же оптимальный план или неразрешима. Вычисления проходят до тех пор, пока не будут исследованы все значения параметра t∈[α, β].
2.66. Для каждого значения параметра t (-∞<t<∞) найти максимальное значение функции
F = Зх1-2х2+5х3-4х5 (21)
при условиях
x1+x2+x3=12-t, (22)
2x1-x2+x4=8+4t
-2x1+2x2+x3=10-6t, (22)
x1,x2,…x5≥0, (23)
Решение. Считая значение параметра t в системе уравнений (22) равным нулю, находим решение задачи (21)-(23) (табл. 1.24) через калькулятор.
Таблица 1.24
| i | базис | Сб | Р0 | 3 | -2 | 5 | 0 | -4 |
| P1 | P2 | P3 | P4 | P5 | ||||
| 1 | Р3 | 5 | 12+t | 1 | 1 | 1 | 0 | 0 |
| 2 | Р4 | 0 | 8+4t | 2 | -1 | 0 | 1 | 0 |
| 3 | Р5 | -4 | 10-6t | -2 | 2 | 0 | 0 | 1 |
| 4 | 20+29t | 10 | -1 | 0 | 0 | 0 | ||
| 1 | Р3 | 5 | 7+4t | 2 | 0 | 1 | 0 | -1/2 |
| 2 | P4 | 0 | 13+t | 1 | 0 | 0 | 1 | 1/2 |
| 3 | P5 | -2 | 5-3t | -1 | -1 | 0 | 0 | 1/2 |
| 4 | 25+26t | 9 | 0 | 0 | 0 | 1/2 |
Как видно из табл. 1.24, Х0*=(0,5-3t,7+4t,13+t,0) при t=0 есть оптимальный план задачи. Очевидно, Х0* является оптимальным планом и тогда, когда среди его компонентов не окажется отрицательных чисел, т.е. при 5-3t≥0; 7+4t≥0; 13+t≥0 или при -7/4≤t≤5/3. Таким образом, если t∈[-7/4; 5/3], то Х0*=(0,5-3t,7+4t,13+t,0)-оптимальный план задачи (21)-(23), при котором Fmax=25+26t.
Исследуем теперь, имеет ли задача оптимальные планы при t>5/3. Если t>5/3, то 5-3t<0 и, следовательно, X=(0,5-3t,7+4t,13+t,0) не является планом задачи. Поэтому при t>5/3 нужно перейти к новому плану, который был бы в тоже время и оптимальным. Это можно сделать в том случае, когда в строке вектора Р2 имеются отрицательные числа х'2j. В данном случае это условие выполняется. Поэтому переходим к новому опорному плану, для чего введем в базис вектор Р1 и исключим из него вектор Р2 (табл. 1.25).
Таблица 1.25
| i | Базис | Сб | Р0 | 3 | -2 | 5 | 0 | -4 |
| P1 | P2 | P3 | P4 | P5 | ||||
| 1 | Рз | 5 | 17-2t | 0 | 2 | 1 | 0 | 1/2 |
| 2 | Р4 | 0 | 18-2t | 0 | 1 | 0 | 1 | 1 |
| 3 | Р1 | 3 | -5+3t | 1 | -1 | 0 | 0 | -1/2 |
| 4 | 70-t | 0 | 9 | 0 | 0 | 5 |
Если t>17/2, то X1=(-5+3t,0,17-2t,18-2t,0) не является планом задачи, так как третья компонента 17-2t есть отрицательное число. Поскольку среди элементов 1-й строки табл. 2.42 нет отрицательных, при t>17/2 исходная задача неразрешима.
Исследуем теперь разрешимость задачи при t<-7/4. В этом случае X=(0,5-3t,7+4t,13+t,0) (см. табл. 2.41) не является планом задачи, так как третья компонента 7+4t есть отрицательное число.
Чтобы при данном значении параметра найти оптимальный план (это можно сделать, так как в строке вектора Р3 стоит отрицательное число -1/2), нужно исключить из базиса вектор Р3 и ввести в базис вектор P5 (табл. 1.26).
Таблица 1.26
| i | Базис | Сб | Р0 | 3 | -2 | 5 | 0 | -4 |
| P1 | P2 | P3 | P4 | P5 | ||||
| 1 | Р5 | -4 | -14-8t | -4 | 0 | -2 | 0 | 1 |
| 2 | Р4 | 0 | 20+5t | 3 | 0 | 1 | 1 | 0 |
| 3 | Р2 | -2 | 12+t | 1 | 1 | 1 | 0 | 0 |
| 4 | 32+30t | 11 | 0 | 1 | 0 | 0 |
Итак, если t∈(-∞, -4), то задача не имеет оптимального плана; если t∈[-4; -7/4], то Х2*=(0,12+t,0,20+2t,-14-8t)- оптимальный план, a Fmax=32+30t; если t∈[-7/4; 5/3], то X0*=(0,5-3t,7+4t,13+t,0)- оптимальный план, a Fmax=25+26t; если t∈[5/3; 17/2], то Х1*=(- 5+3t,0,17-2t, 18-21,0)-оптимальный план, a Fmax =70-t; если t∈(17/2; +∞), то задача неразрешима.
Решение задачи, целевая функция и правые части ограничений которой содержат параметр. Используя описанные выше алгоритмы решения задач параметрического программирования, можно найти решение задачи, в которой от параметра t линейно зависят как коэффициенты целевой функции, так и свободные члены системы уравнений.
Задача 3. Найти максимальное значение функции
F=(8-5t)x1+(9-3t)x2+(-3+5t)x3-(2+4t)x4
при условиях
x1-x2+x3=24-12t
-x1+2x2+x4=-18+10t
x1, x2≥0, t∈(-∞, +∞)
Решение. Считая значение параметра t равным числу 2 ( число 2 взято произвольно), находим симплексным методом решение полученной задачи линейного программирования (табл. 1.27).
Таблица 1.27
| i | Базис | Сб | Р0 | 8-5t | 9-3t | -3+5t | -2-4t |
| P1 | P2 | Р3 | P4 | ||||
| 1 | Р3 | -3-5t | 24-12t | 1 | -1 | 1 | 0 |
| 2 | Р4 | -2-4t | -18+10t | -1 | 2 | 0 | 1 |
| 3 | -36+28t-100t2 | 14t-9 | -10t-10 | 0 | 0 | ||
| 1 | Р3 | -3+5t | 15-7t | 1/2 | 0 | 1 | 1/2 |
| 2 | P2 | 9-3t | -9+5t | -1/2 | 1 | 0 | 1/2 |
| 3 | -126+168t-50t2 | 9t-14 | 0 | 0 | 5t+5 |
Найденный вектор Х0* является оптимальным планом задачи при 15-7t≥0 и -9+5t≥0, т.е. 9/5 ≤t≤15/7. Итак, если 9/5 ≤t≤15/7, то Х0*=(0, 15-7t,-9+5t,0)-оптимальный план задачи, при котором Fmax=-126+168-50t2.
Если t<9/5, то -9+5t<0 и вектор X=(0,-9+5t,15-7t,0) не является планом задачи.
Поэтому при t<9/5 следует перейти к новой симплекс-таблице, что можно сделать, так как в строке вектора Р2 (табл. 1.27) имеется отрицательное число -1/2. Рассматривая это число как разрешающий элемент, переходим к новой симплекс-таблице, для чего исключим из базиса вектор Р2 и введем вместо него вектор P1 (табл. 1.28).
Таблица 1.28
| i | Базис | Cб | Р0 | 8-5t | 9-3t | -3+5t | -2-4t |
| P1 | P2 | Р3 | P4 | ||||
| 1 | Р3 | -3+5t | 6-2t | 0 | 1 | 1 | 1 |
| 2 | P1 | 8-5t | 18-10t | 1 | -2 | 0 | -1 |
| 3 | 126-134t+40t2 | 0 | -28+18t | 0 | 14t-9 |
Рассмотрим теперь значение параметра t>15/7. При этих значениях вектор X=(0,-9+5t,15-7t,0) уже не является оптимальным планом задачи, поскольку 15-7t<0. Так как в строке вектора Р3 (табл. 1.28) нет отрицательных чисел, то при t>15/7 задача неразрешима.
Мы нашли решение задачи при изменении параметра t от 14/9 до +∞. Рассмотрим теперь значения параметра от -∞ до 14/9. Если t<14/9, то в последней строке табл. 1.28 имеется отрицательное число 18t-28. Поэтому следует перейти к новому опорному плану, введя в базис вектор Р2 и исключив из него вектор Р3 (табл. 1.29).
Таблица 1.29
| i | Базис | Cб | Р0 | 8-5t | 9-3t | -3+5t | -2-4t |
| P1 | P2 | Р3 | P4 | ||||
| 1 | Р2 | 9-3t | 6-2t | 0 | 1 | 1 | 1 |
| 2 | P1 | 8-5t | 30-14t | 1 | 0 | 2 | 1 |
| 3 | 294-98t+76t2 | 0 | 0 | 28-18t | 19-4t |
Итак, при t∈(-∞; 14/9] задача имеет оптимальный план X2*=(30-14t,6-2t,0,0); при t∈[14/9; 9/5] - X1*=(18-10t,0,6-2t,0); при t∈[9/5; 15/7] - X0*=(0,-9+5t, 15-7t,0); при t>15/7 она не разрешима.

