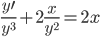Численные методы поиска экстремума функций многих переменных
Метод поиска:- Градиентный метод с постоянным шагом (без ограничений).
- Градиентный метод с переменным шагом (без ограничений).
- Метод наискорейшего спуска (без ограничений).
- Метод сопряженных направлений (без ограничений).
- Метод сопряженных направлений (при наличии ограничений).
Вид ограничений: x1+x2-1=0
Координаты начальной точки x0=(3;-2)
Этапы проектирования
- Постановка задачи в соответствии с вариантом задания.
- Представление заданной квадратичной формы в матричной форме записи.
- Исследование характера экстремума.
- Описание в матричной форме метода поиска и составление алгоритма.
- Составление структурной схемы алгоритма поиска.
- Программирование в среде Math Cad.
- Расчет.
- Выводы по работе.
Постановка и решение задач многомерной безусловной оптимизации
Задачи многомерной безусловной минимизации
Для заданной функции решить задачу многомерной безусловной минимизации f(x1, x2), x∈X (X⊂R) и начальной точки x0.Пусть f(x) = f(x1, x2, … ,xn) – действительная функция n переменных, определенная на множестве X Ì Rn. Точка x* Î X называется точкой локального минимума f(x) на множестве X, если существует такая
e-окрестность этой точки, что для всех x из этой окрестности, т. е., если
|| x - x*|| < e, выполняется условие f(x*) £ f(x).
Если выполняется условие f(x*) < f(x), то x* называется точкой строгого локального минимума. У функции может быть несколько локальных минимумов. Точка x*Î X называется точкой глобального минимума f(x) на множестве X, если для всех x Î X выполняется условие f(x*) £ f(x). Значение функции f(x*) называется минимальным значением f(x) на множестве X. Для нахождения глобального минимума необходимо найти все локальные минимумы и выбрать наименьшее значение. В дальнейшем будем рассматривать задачу нахождения локального минимума.
Теорема 1 (необходимое условие экстремума)
Пусть x*∈Rn есть точка локального минимума (максимума) функции f(x) на множестве Rn и она дифференцируема в точке х*. Тогда градиент функции в точке х* равен нулю:
▽f(x*)=0
Теорема 2 (достаточное условие)
Пусть функция f(x) в точке х* дважды дифференцируема, ее градиент равен нулю, а матрица Гессе является положительно определенной (отрицательно определенной), т. е. ▽f(x*)=0.
H(x*)>0 (H(x*)<0)
Тогда точка х* есть точка локального минимума (максимума) функции на множестве Rn.
Для определения знака матрицы Гессе используется критерий Сильвестра.
Задание 1
Найти минимум функции классическим методом, используя необходимые и достаточные условия.
Данную задачу будем решать для функции f(x1,x2).
Начальная точка x0
f(x)=3x21+x22-x1x2+x1; x0=(1.5,1.5)
Найдем частные производные первого порядка функции f(x):
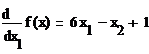
![]()
![]() ;
; ![]() ;
; 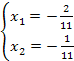 ;
;
Найдем производные второго порядка функции f(x):
![]()
![]()
![]()
Классифицируем матрицу Гессе, используя критерий Сильвестра:
Δ1=11>0
Δ2=6>0
Следовательно, матрица является положительно определенной.
Используя критерии проверки достаточных условий экстремума, можно сделать вывод: точка ![]() - является точкой локального минимума.
- является точкой локального минимума.
Значение функции в точке минимума:
![]() ;
;
![]()
![]()
Задание 2
Найти минимум данной функции методом градиентного спуска с дроблением шага.
Метод градиентного спуска с дроблением шага
Метод градиентного спуска является одним из самых распространенных и самых простых методов решения задачи безусловной оптимизации. Он основан на свойстве градиента функции, согласно которому направление градиента совпадает с направлением наискорейшего возрастания функции, а направление антиградиента – с направлением наискорейшего убывания функции. При решении задачи безусловной минимизации за направление спуска из точки x(m) выбирается
p(m) = –g(x(m)) = –f '(x(m)).
Таким образом, итерационная процедура для этого метода имеет вид
x(m+1) = x(m) – a(m)g(x(m)) (*)
Для выбора шага a(m) можно использовать процедуру дробления шага, которая состоит в следующем. Произвольно фиксируют начальное значение шага a(m) = a(m – 1) = a. Если в точке x(m+1), вычисленной в соответствии с (2.24), выполняется неравенство
f(x(m+1)) > f(x(m)),
то шаг дробится, например, пополам, т.е. полагается a(m +1) = 0.5a(m).
Применим метод градиентного спуска с дроблением шага для минимизации квадратичной функции
f(x) = ½(Ax, x) + (b, x) + c
с симметричной положительно определенной матрицей A.
Алгоритм метода градиентного спуска с дроблением шага для квадратичной функции
Шаг 1. Для квадратичной функции f(x) = ![]()
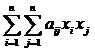 +
+ 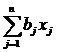 + с, ввести матрицу A =(aij), вектор b = (b1, b2, … , bn)T и коэффициент c,
+ с, ввести матрицу A =(aij), вектор b = (b1, b2, … , bn)T и коэффициент c,
i = 1, … , n; j = 1, … , n.
Выбрать произвольную начальную точку x = (x1, x2, … , xn)T, например,
x = (0, 0, … , 0)T, начальный шаг a и e > 0. Вычислить f(x).
Шаг 2. Вычислить g = f '(x) = Ax + b, или покоординатно
g = (g1, g2, … , gn)T,
gi = 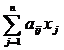 + bi, i = 1, …, n.
+ bi, i = 1, …, n.
Шаг 3. Проверить выполнение критерия окончания вычислений:
||f '(x)|| < e.
Если это условие выполнено, вычисления закончить и за приближенное значение точки минимума принять точку
x* = x = (x1, x2, … , xn)T.
В противном случае перейти к шагу 4.
Шаг 4. Вычислить
y = (y1, y2, … , yn), yi= xi– a gi, i = 1, …, n.
Шаг 5. Вычислить f(y).
Шаг 6. Если f(y) < f(x), то положить x = y, f(x) = f(y) и перейти к шагу 2, иначе – перейти к шагу 7.
Шаг 7. Положить α=α/2 и перейти к шагу 4.
Реализация задачи в пакете MathCAD 14
Данную задачу мы решаем для следующей функции:f(x1,x2)=3x12+x22-x1x2+x1
Задание функции, реализующей метод дробления шага:
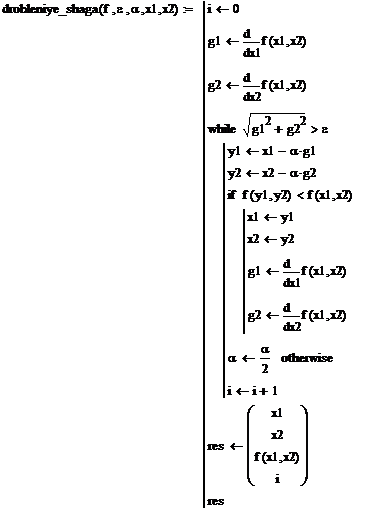
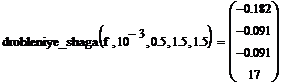
В результате решения данной задачи был найден минимум
x* = (-0.182; -0.091),
значение функции f(x*) = -0.091,
количество итераций n = 17.