Решение СЛАУ методом LU-разложения
Назначение сервиса. Сервис предназначен для решения системы линейных уравнений методом декомпозиции (иначе LU-разложением). Данный метод также носит название метод Халецкого (см. пример решения).
Инструкция. Для решения СЛАУ методом декомпозиции выберите
Пусть система уравнений задается в виде:
Ax = d, (1)
где A - квадратная матрица nxn. Представим матрицу A в виде произведения нижней треугольной матрицы B и верхней треугольной матрицы C с единичной диагональю.
A = BC (2)
Тогда система (1) может быть представлена в виде двух систем с треугольными матрицами:
By = d; Cx = y (3)
Системы (3) решаются через формулы:
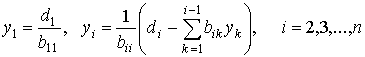 .
.
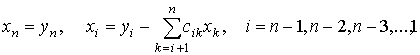 .
.
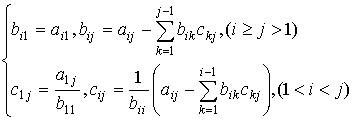 (4)
(4)Пример №1. Дана система линейных уравнений. Решить ее методом LU-разложения.
Решение. Алгоритм декомпозиции основан на идее представления исходной матрицы в виде произведения двух треугольных матриц. Пусть задана квадратная матрица:
Представим A в виде: A=BC
Покажем пример вычислений нескольких значений матриц B и C.
Вычисляем значение элемента b11=1
c11=1/1=1
c12=3/1=3
c13=3/1=3
Вычисляем значение элемента b21=1
Вычисляем значение элемента b22=-2 - (1 • 3)=-5
c22=-5/(-5)=1
c23=0/(-5)=0
Вычисляем значение элемента b31=3
Вычисляем значение элемента b32=3 - (3 • 3)=-6
Вычисляем значение элемента b33=-1 - (3 • 3 -6 • 0)=-10
c33=-10/(-10)=1
| B= |
|
| C= |
|
Вычисляем значения yi
y1 = 11/1 = 11
y2 = (1 - 1 • 11 )/(-5) = 2
y3 = (1 - 3 • 11 -6 • 2 )/(-10) = 2
Вычисляем значения xi
x3 = y3 = 2
x2 = 2 - (0 • 2 ) = 2
x1 = 11 - (3 • 2 + 3 • 2 ) = -1
Пример №2. Решить систему уравнений Ax = b методом Гаусса (LU-разложения).