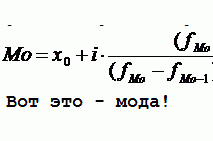Методика статистического изучения преступности
Число зарегистрированных преступлений по видам (тысяч)| 1990 | 2000 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | |
| Зарегистрировано преступлений - всего | 1839,5 | 2952,4 | 3554,7 | 3855,4 | 3582,5 | 3209,9 | 2994,8 | 2628,8 | 2404,8 |
| в том числе: | |||||||||
| убийство и покушение на убийство | 15,6 | 31,8 | 30,8 | 27,5 | 22,2 | 20,1 | 17,7 | 15,6 | 14,3 |
| умышленное причинение тяжкого вреда здоровью | 41,0 | 49,8 | 57,9 | 51,4 | 47,3 | 45,4 | 43,1 | 39,7 | 38,5 |
| изнасилование и покушение на изнасилование | 15,0 | 7,9 | 9,2 | 8,9 | 7,0 | 6,2 | 5,4 | 4,9 | 4,8 |
| грабеж | 83,3 | 132,4 | 344,4 | 357,3 | 295,1 | 244,0 | 205,4 | 164,5 | 127,8 |
| разбой | 16,5 | 39,4 | 63,7 | 59,8 | 45,3 | 35,4 | 30,1 | 24,5 | 20,1 |
| кража | 913,1 | 1310,1 | 1573,0 | 1677,0 | 1567,0 | 1326,3 | 1188,6 | 1108,4 | 1038,6 |
| терроризм, единиц | ... | 135 | 203 | 112 | 48 | 10 | 15 | 31 | 29 |
| преступления, связанные с незаконным оборотом наркотиков | 16,3 | 243,6 | 175,2 | 212,0 | 231,2 | 232,6 | 238,5 | 222,6 | 215,2 |
| нарушения правил дорожного движения и эксплуатации транспортных средств | 96,3 | 52,7 | 26,6 | 26,3 | 25,6 | 24,3 | 27,5 | 26,3 | 27,3 |
| из них повлекшие по неосторожности смерть человека, двух или более лиц | 15,9 | 15,4 | 15,7 | 15,8 | 15,5 | 13,6 | 10,6 | 10,3 | 10,9 |
| взяточничество | 2,7 | 7,0 | 9,8 | 11,1 | 11,6 | 12,5 | 13,1 | 12,0 | 11,0 |
Для расчета показателей динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем. Исчисляемые при этом показатели называются базисными.
Для расчета показателей динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким способом показатели динамики называются цепными.
Важнейшим статистическим показателем динамики является абсолютный прирост, который определяется в разностном сопоставлении двух уровней ряда динамики в единицах измерения исходной информации.
Абсолютный прирост
цепной прирост: ∆yц = yi - yi-1
базисный прирост: ∆yб = yi - y1
Темпы прироста характеризуют абсолютный прирост в относительных величинах. Исчисленный в процентах темп прироста показывает, на сколько процентов изменился сравниваемый уровень с уровнем, принятым за базу сравнения.
Темп прироста
цепной темп прироста: Tпрцi = ∆yi / yi-1
базисный темп прироста: Tпpб = ∆yбi / y1
Распространенным статистическим показателем динамики является темп роста. Он характеризует отношение двух уровней ряда и может выражаться в виде коэффициента или в процентах.
Темп роста
цепной темп роста: Tpцi = yi / yi-1
базисный темп роста: Tpб = yбi / y1
Абсолютное значение 1% прироста
цепной: 1%цi = yi-1 / 100%
базисный: 1%б = yб / 100%
Темп наращения
Важным статистическим показателем динамики социально-экономических процессов является темп наращивания, который в условиях интенсификации экономики измеряет наращивание во времени экономического потенциала
Tн = ∆yцi / y1
Таблица 1 - Цепные показатели ряда динамики.
| Период | Число зарегистрированных преступлений в РФ, тыс. | Абсолютный прирост | Темп прироста, % | Темпы роста, % | Абсолютное содержание 1% прироста | Темп наращения, % |
| 2005 | 3554.7 | 0 | 0 | 100 | 35.55 | 0 |
| 2006 | 3855.4 | 300.7 | 8.46 | 108.46 | 35.55 | 8.46 |
| 2007 | 3582.5 | -272.9 | -7.08 | 92.92 | 38.55 | -7.68 |
| 2008 | 3209.9 | -372.6 | -10.4 | 89.6 | 35.83 | -10.48 |
| 2009 | 2994.8 | -215.1 | -6.7 | 93.3 | 32.1 | -6.05 |
| 2010 | 2628.8 | -366 | -12.22 | 87.78 | 29.95 | -10.3 |
| 2011 | 2404.8 | -224 | -8.52 | 91.48 | 26.29 | -6.3 |
| Итого | 22230.9 |
Базисные показатели ряда динамики количества правонарушений оформим в виде таблицы 2.
| Период | Количество зарегистрированных преступлений в России, тыс. | Абсолютный прирост | Темп прироста, % | Темпы роста, % |
| 2005 | 3554.7 | 0 | 0 | 100 |
| 2006 | 3855.4 | 300.7 | 8.46 | 108.46 |
| 2007 | 3582.5 | 27.8 | 0.78 | 100.78 |
| 2008 | 3209.9 | -344.8 | -9.7 | 90.3 |
| 2009 | 2994.8 | -559.9 | -15.75 | 84.25 |
| 2010 | 2628.8 | -925.9 | -26.05 | 73.95 |
| 2011 | 2404.8 | -1149.9 | -32.35 | 67.65 |
| Итого | 22230.9 |
Расчет средних характеристик рядов.
Средний уровень ряда y динамики характеризует типическую величину абсолютных уровней
Средний уровень ряда динамики
![]()
В среднем за исследуемый период ежегодно количество зарегистрированных преступлений составляло на уровне 3175.84 тыс.
Средний темп роста
![]()
Средний темп прироста
Tnp = 0.94 - 1 = -0.06
Средний абсолютный прирост
![]()
Вывод: В среднем за весь период с 2005 по 2011 гг. рост числа зарегистрированных преступлений составил 0.94 (т.е. они сокращались на 6% ежегодно или на 191.65 тыс.).
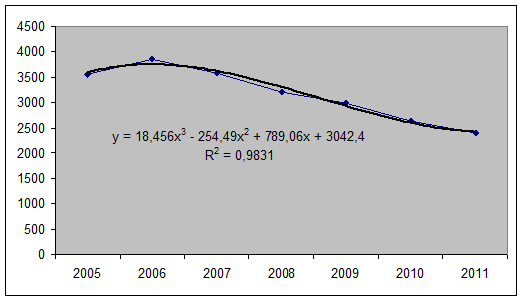
После анализа динамики спрогнозируем число правонарушений на следующие периоды. Для этого представим исходные данные в виде графика.
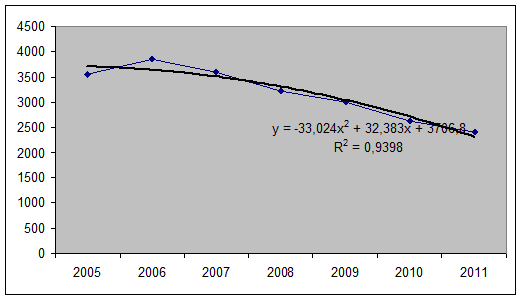
При выборе вида функции тренда можно воспользоваться методом конечных разностей (обязательным условием применения данного подхода является равенство интервалов между уровнями ряда).
Конечными разностями первого порядка являются разности между последовательными уровнями ряда:
Δ1t = Yt - Yt-1
Конечными разностями второго порядка являются разности между последовательными конечными разностями 1-го порядка:
Δ2t = Δ1t - Δ1t-1
Конечными разностями j-го порядка являются разности между последовательными конечными разностями (j–1)-го порядка:
Δjt = Δj-1t - Δj-1t-1
Если общая тенденция выражается линейным уравнением Y = a + bt, тогда конечные разности первого порядка постоянны: Δ12 = Δ13 = ... = Δ1n, а разности второго порядка равны нулю.
Если общая тенденция выражается параболой второго порядка: Y = a+ bt + ct2, то получим постоянными конечные разности второго порядка: Δ23 = Δ24 = ... = Δ2n, нулевыми – разности третьего порядка.
Если примерно постоянными оказываются темпы роста, то для выравнивания применяется показательная функция.
При выборе формы уравнения следует исходить из объема имеющейся информации. Чем больше параметров содержит уравнение, тем больше должно быть наблюдений при одной и той же степени надежности оценивания.
Выбор формы кривой может осуществляться и на основе принятого критерия качества уравнения регрессии, в качестве которого может служить сумма квадратов отклонений фактических значений уровня ряда от значений уровней, рассчитанных по уравнению тренда.
Из совокупности кривых выбирается та, которой соответствует минимальное значение критерия. Другим статистическим критерием является коэффициент множественной детерминации R2.
Таблица 3 – Расчет конечных разностей
| yi | Δ1t | Δ2t | Темп роста |
| 3554.7 | - | - | - |
| 3855.4 | 300.7 | - | 1.08 |
| 3582.5 | -272.9 | -573.6 | 0.93 |
| 3209.9 | -372.6 | -99.7 | 0.9 |
| 2994.8 | -215.1 | 157.5 | 0.93 |
| 2628.8 | -366 | -150.9 | 0.88 |
| 2404.8 | -224 | 142 | 0.91 |
1. Находим параметры уравнения методом наименьших квадратов.
Система уравнений МНК:
a0n + a1∑t + a2∑t2 = ∑y
a0∑t + a1∑t2 + a2∑t3 = ∑yt
a0∑t2 + a1∑t3 + a2∑t4 = ∑yt2
Таблица 4 – Данные для расчета МНК
| t | y | t2 | y2 | t•y | t3 | t4 | t2 y |
| 1 | 3554.7 | 1 | 12635892.09 | 3554.7 | 1 | 1 | 3554.7 |
| 2 | 3855.4 | 4 | 14864109.16 | 7710.8 | 8 | 16 | 15421.6 |
| 3 | 3582.5 | 9 | 12834306.25 | 10747.5 | 27 | 81 | 32242.5 |
| 4 | 3209.9 | 16 | 10303458.01 | 12839.6 | 64 | 256 | 51358.4 |
| 5 | 2994.8 | 25 | 8968827.04 | 14974 | 125 | 625 | 74870 |
| 6 | 2628.8 | 36 | 6910589.44 | 15772.8 | 216 | 1296 | 94636.8 |
| 7 | 2404.8 | 49 | 5783063.04 | 16833.6 | 343 | 2401 | 117835.2 |
| 28 | 22230.9 | 140 | 72300245.03 | 82433 | 784 | 4676 | 389919.2 |
7a0 + 28a1 + 140a2 = 22230.9
28a0 + 140a1 + 784a2 = 82433
140a0 + 784a1 + 4676a2 = 389919.2
Получаем a0 = -33.02, a1 = 32.38, a2 = 3706.79
Уравнение тренда:
y = -33.02t2+32.38t+3706.79
Эмпирические коэффициенты тренда a и b являются лишь оценками теоретических коэффициентов βi, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных.
Оценим качество уравнения тренда с помощью ошибки абсолютной аппроксимации.
![]()
Ошибка аппроксимации в пределах 5%-7% свидетельствует о хорошем подборе уравнения тренда к исходным данным.
Поскольку ошибка меньше 7%, то данное уравнение можно использовать в качестве тренда.
Однофакторный дисперсионный анализ.
Средние значения
Дисперсия
Среднеквадратическое отклонение
Коэффициент эластичности представляет собой показатель силы связи фактора t с результатом у, показывающий, на сколько процентов изменится значение у при изменении значения фактора на 1%.
Коэффициент эластичности меньше 1. Другими словами – Y (число зарегистрированных преступлений в РФ) не зависит от времени .
Эмпирическое корреляционное отношение вычисляется для всех форм связи и служит для измерение тесноты зависимости. Изменяется в пределах [0;1].
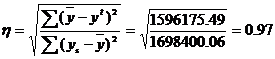
где ∑(k-yt)² = 1698400.06-102224.57 = 1596175.49
В отличие от линейного коэффициента корреляции он характеризует тесноту нелинейной связи и не характеризует ее направление. Изменяется в пределах [0;1].
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 < η < 0.3: слабая;
0.3 < η < 0.5: умеренная;
0.5 < η < 0.7: заметная;
0.7 < η < 0.9: высокая;
0.9 < η < 1: весьма высокая;
Полученная величина свидетельствует о том, что изменение временного периода t существенно влияет на y.
Индекс детерминации.
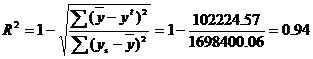
т.е. в 93.98% случаев влияет на изменение данных. Другими словами - точность подбора уравнения тренда - высокая.
| t | y | y(t) | (y-y)2 | (y-y(t))2 | (y-y(t)) : y |
| 1 | 3554.7 | 3706.15 | 143532.73 | 22935.66 | 0.0426 |
| 2 | 3855.4 | 3639.46 | 461797.91 | 46631.32 | 0.056 |
| 3 | 3582.5 | 3506.72 | 165370.03 | 5742.39 | 0.0212 |
| 4 | 3209.9 | 3307.94 | 1159.89 | 9611.47 | 0.0305 |
| 5 | 2994.8 | 3043.11 | 32776.52 | 2333.58 | 0.0161 |
| 6 | 2628.8 | 2712.23 | 299255.89 | 6960.33 | 0.0317 |
| 7 | 2404.8 | 2315.3 | 594507.09 | 8009.82 | 0.0372 |
| 28 | 22230.9 | 22230.9 | 1698400.06 | 102224.57 | 0.24 |
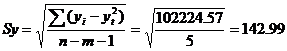
где m = 1 - количество влияющих факторов в модели тренда.
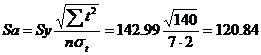
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;α/2) = (5;0.025) = 2.571
Интервальный прогноз.
Определим среднеквадратическую ошибку прогнозируемого показателя.
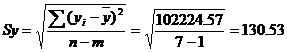
m = 1 - количество влияющих факторов в уравнении тренда.
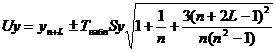 ·
·
где L - период упреждения; уn+L - точечный прогноз по модели на (n + L)-й момент времени; n - количество наблюдений во временном ряду; Sy - стандартная ошибка прогнозируемого показателя; Tтабл - табличное значение критерия Стьюдента для уровня значимости α и для числа степеней свободы, равного n-2.
Точечный прогноз числа преступлений в РФ на 2012 год, t = 8: y(8) = -33.02*82 + 32.38*8 + 3706.79 = 1852.33
K1 = 439.39
1852.33 - 439.39 = 1412.94 ; 1852.33 + 439.39 = 2291.72
Интервальный прогноз:
t = 8: (1412.94;2291.72)
Точечный прогноз количества зарегистрированных правонарушений в России на 2013 год, t = 9: y(9) = -33.02*92 + 32.38*9 + 3706.79 = 1323.31
K2 = 478.82
1323.31 - 478.82 = 844.49 ; 1323.31 + 478.82 = 1802.13
Интервальный прогноз:
t = 9: (844.49;1802.13)
3. Проверка гипотез относительно коэффициентов линейного уравнения тренда.
1) t-статистика. Критерий Стьюдента.
Статистическая значимость коэффициента b не подтверждается
Статистическая значимость коэффициента a не подтверждается
Доверительный интервал для коэффициентов уравнения тренда.
Определим доверительные интервалы коэффициентов тренда, которые с надежность 95% будут следующими:
(b - tнабл Sb; b + tнабл Sb)
(-33.02 - 2.571•27.02; -33.02 + 2.571•27.02)
(-102.5;36.45)
(a - tнабл Sa; a + tнабл Sa)
(32.38 - 2.571•120.84; 32.38 + 2.571•120.84)
(-278.31;343.08)
Так как точка 0 (ноль) лежит внутри доверительного интервала, то интервальная оценка коэффициента a статистически незначима.
2) F-статистика. Критерий Фишера.
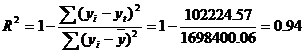
Fkp = 6.61
где m - количество факторов в уравнении тренда (m=1).
Поскольку F > Fkp, то коэффициент детерминации (и в целом уравнение тренда) статистически значим
Вывод: не смотря на то, что полученное уравнение тренда статистически значимо (по критерию Фишера), использовать его для прогноза числа преступлений не рекомендуется.
Если следовать этой модели, то через 5 лет число зарегистрированных правонарушений в России сократится до нуля. Скорей всего в данном случае применима полиномиальная модель третьей степени.
Список литературы
- Правовая статистика: учебник. Издательство: ЮНИТИ-ДАНА, 2010 г.
- Лунеев В.В. Юридическая статистика. М. Юристъ. 1999. 400 с.
- Юридическая статистика: Учебное пособие. Селезнев А.В., Сысоев Э.В., Терехов А.В., Рак И.П. Тамбов: Изд-во Тамб. гос. техн. ун-та. 2004г.
- Сафаров Н.А. Математические методы оценки состояния и прогнозирования преступности: Монография. Харьков Ун-т внутр дел. 1998 г. 158 с.
- Забрянский Г.И. Методика статистического изучения преступности. Учебное пособие. Краснодар: Изд-во Кубан. ун-та. 1976 г.