Двухфазный симплекс-метод
Двухфазный симплекс-метод (или двухэтапный метод относится к методам искусственного базиса) применяется в тех случаях, когда в задаче ЛП в канонической форме затруднительно определить начальное допустимое базисное решение с помощью элементарных преобразований (привести систему к диагональному виду).
Инструкция. Выберите количество переменных и количество строк (количество ограничений). Полученное решение сохраняется в файле Word и Excel.
При этом ограничения типа xi ≥ 0 не учитывайте. Если в задании для некоторых xi отсутствуют ограничения, то ЗЛП необходимо привести к КЗЛП, или воспользоваться этим сервисом.
Пример. Следующую задачу ЛП решить двухфазным симплекс-методом:
f(x)=x1–x2+1→min, (1)
при ограничениях
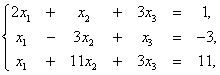 (2)
(2)Первая фаза (цель: при помощи искусственного базиса и симплекс-метода определить базисные переменные из числа исходных переменных).
В систему (2) вводим искусственные переменные x4 ≥0, x 5 ≥0, x6 ≥0, (предварительно умножив обе части второго неравенства на -1), новую целевую функцию, как сумму всех искусственных переменных, а старую присоединяем – к ограничениям:
z(x)=x4+x5+x6, (4)
при ограничениях:
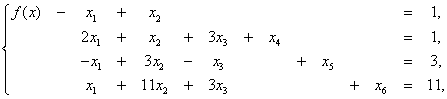 , (5)
, (5)x1, ..., x6≥0, (6)
Искусственные переменные x4, x5, x6 выбираем в качестве базисных, а все остальные x1, x2, x3 - в качестве небазисных. По правилу симплекс-метода исключаем базисные переменные из целевой функции (4) (при помощи уравнений системы (5) , содержащих эти переменные):
z(x)=-2x1–15x2-5x3+15
или, что все равно,
z(x)+2x1+15x2+5x3=15, (7)
Начальное допустимое базисное решение: x0 = (x01, x02, x03, x04, x05, x06) = (0,0,0,1,3,11)
называется искусственным базисом. При помощи этого базиса и выражений (7) , (5) строим начальную симплекс-таблицу I-ой фазы.
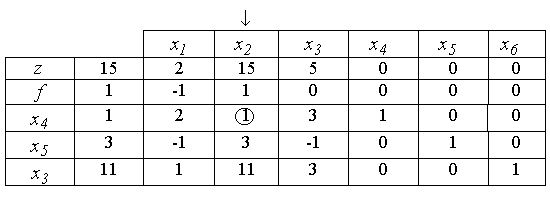
До конца первой фазы роль нулевой строки играет строка z , все остальное – как в симплекс-методе. Следует только заметить, что строка для f(x) не участвует в выборе ведущей строки.
Из (4) видно, что min z(x)=0 и достигается при x4=x5=x6=0, т.е. задача (4) будет решена, если все искусственные переменные будут вытеснены из базиса, а z=0 . Это и будет означать конец первой фазы и переход ко второй фазе.
Обратите внимание, что в первой таблице ведущей может быть любая из последних трех строк (предвестник зацикливания). В таких случаях можно выбрать любой из них - выберем первую строку.
Так как искусственная переменная x4 выходит из базиса, то соответствующий столбик в дальнейшем можно исключить.
В результате соответствующих преобразований получим вторую симплекс-таблицу.
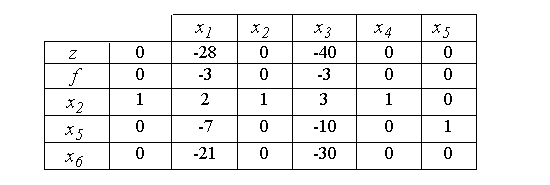
Из таблицы следует, что min z достигнут, однако искусственные переменные x6 и x5 еще не выведены из базиса. В такой ситуации правила симплекс-метода "не работают" (так как ввиду отсутствия в нулевой строке положительных оценок нельзя выбрать ведущий столбик). Задача здесь одна - вывести оставшиеся искусственные переменные из базиса. Выведем сначала x5. Умножим все элементы этой строки на -1 (что допустимо, так как в нулевом столбике стоит 0). Введем в базис вместо x5 переменную x1 . С этой целью строку для x5 поделим на 7 и с "ведущим элементом" 1 выполним элементарные преобразования (как в симплекс-методе). В результате получим таблицу:
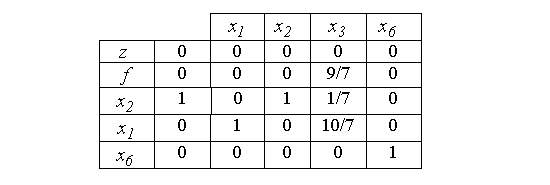
Остается в базисе еще x6 . Ее из числа базисных вывести нельзя, так как все элементы этой строки равны нулю, кроме 1 в столбике для x6. Это говорит о том, что в системе (2) третье уравнение было "лишним", и потому последнюю строку таблицы можно вычеркнуть. Действительно, третье уравнение (2) является линейной комбинацией первых двух (оно получается вычитанием второго уравнения, умноженного на 3, из первого уравнения, умноженного на 2).
Вычеркивая столбик x6 и строку для z , приходим к таблице

содержащей только элементы исходной задачи (1)-(3) и с базисными переменными из числа исходных переменных. Таким образом, цель первой фазы выполнена.
Вторая фаза (цель: применяя обычный симплекс-метод к полученной в результате первой фазы таблице, получить оптимальное решение исходной задачи).
Допустимое базисное решение для последней таблицы есть x0=(0,1,0) . Заметим, что это вырожденное д.б.р., так как в нем базисная переменная x1=0, т.е. здесь мы можем получить зацикливание.
В качестве упражнения вторую фазу предлагается сделать самостоятельно.
Теперь можно привести алгоритм двухфазного симплекс-метода:
1. привести задачу ЛП к канонической форме;
2. ввести в ограничения искусственные переменные и составить новую целевую функцию z;
3. исключить из новой целевой функции все искусственные переменные;
4. используя искусственные переменные в качестве базисных, построить начальную симплекс-таблицу;
5. применить симплекс-метод, исключая из таблиц столбцы для искусственных переменных по мере их выхода из базиса до тех пор, пока min z=0 и все искусственные переменные не будут выведены из базиса;
6. вычеркнуть строчку для z и перейти ко второй фазе;
7. во второй фазе к таблице, полученной в результате первой фазы, применять симплекс-метод до тех пор, пока не найдется оптимальное решение исходной задачи или не выявится его отсутствие.
Примечания к двухфазному симплекс-методу.
1. Если в результате первой фазы окажется, что min z>0, то система ограничений исходной задачи (в канонической форме) несовместна. Во всех остальных случаях первая фаза разрешима.
2. Если min z=0 и в таблице остались искусственные переменные, то, используя элементарные преобразования, эти переменные следует вывести из базиса, а вместо них ввести исходные переменные.
3. Пусть каноническая форма задачи ЛП получена с помощью слабых переменных. Применение двухфазного симплекс-метода упростится, если искусственные переменные ввести только в те ограничения, в которых слабая переменная либо отсутствует (исходное ограничение - равенство), либо не может войти в базис (введена в ограничение со знаком минус).


