Матричное описание симплекс-метода
Рассмотрим каноническую ЗЛП в матричной форме:Ах = b, х ≥ 0.
Рассмотрим сначала случай, когда строки матрицы A линейно независимые. Пусть B — некоторая база матрицы A, а B — соответствующая базисная подматрица и пусть
A = (B,N)
c = (cB, cN)
где через xB, cB обозначены векторы, составленные из базисных компонент векторов x и c соответственно, а через xN,
cN обозначены векторы, составленные из небазисных компонент
векторов x и c соответственно. Тогда ЗЛП примет вид:
BxB + NxN = b, xB ≥ 0, xN ≥ 0.
Шаг исключения Гаусса на каждой итерации симплекс-метода заключается в умножении слева текущей симплексной таблицы на матрицу
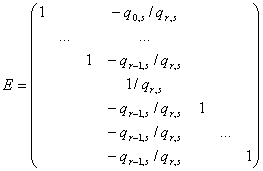
M = Et· Et-1 · …· E1
Матрица M имеет следующее блочное строение:
Пусть на некоторой итерации симплекс-метода получена симплекс-таблица
Справедливы следующие равенства, выражающие элементы симплексной таблицы через коэффициенты ограничений и вектор цен:
q00 = cx = ub, b* = B-1b, c*= c —u A, а* = B-1as.
Интерпретируя коэффициенты симплекс-таблицы, получим следующую эквивалентную формулировку задачи:
xB = B -1 b – B -1 NxN
xB ≥ 0 , xN ≥ 0
Формула с* = c - uA показывает, что для того, чтобы вычислить текущие относительные оценки (нулевую строку симплекс-таблицы) необходимо из строки c вычесть все строки матрицы A, домноженные на соответствующие цены u.
Решение х системы Ax = b базисное, если хN = 0 и, следовательно, xB = В-1b. Базисное решение х допустимо, если х ≥ 0 и, так как х N = 0, то достаточно потребовать х B ≥ 0. Значение целевой функции cx на базисном решении х есть сх = ub. Базисное решение оптимально, если c * = c — uA ≥ 0, или с N= cN — uN ≥ 0.



